Ruheenergie und Gesamtenergie

In der klassischen Physik setzt sich die Energie eines Körpers additiv aus den Energieformen zusammen, die er hat. Masse und Energie sind voneinander unabhängige Größen.
In relativistischer Betrachtungsweise spielt wegen der Äquivalenz von Masse und Energie die Masse des Körpers für die ihm zuzuordnende Energie eine wichtige Rolle. Dabei ist zwischen seiner Ruheenergie und seiner Gesamtenergie zu unterscheiden.

Energie in der klassischen Physik

In der klassischen Physik setzt sich die Energie eines Körpers additiv aus den Energieformen zusammen, die er hat. So besitzt z.B. der in Bild 1 abgebildete Felsen aufgrund seiner Lage potenzielle Energie und innere Energie. Daraus ergibt sich seine Gesamtenergie.
Die kinetische Energie eines Körpers hängt von seiner Masse und seiner Geschwindigkeit ab, wobei die Masse als konstant angesehen wird.
Die thermische Energie eines Körpers wird durch seine Masse und seine Temperatur bestimmt. Für ein abgeschlossenes System gilt der Energieerhaltungssatz. Ein unmittelbarer Zusammenhang zwischen Energie und Masse besteht dagegen in der klassischen Physik nicht. Beide Größen sind unabhängig voneinander.

Ruheenergie und Gesamtenergie - Steine

Raum, B., Neuenhagen

Energie aus relativistischer Sicht

Aufgrund der Beziehung $E = m \cdot c^{2}$ kann einem ruhenden Körper mit bestimmter Masse eine Energie zugeordnet werden.

Die Energie, die ein Körper im Ruhezustand aufgrund seiner Masse besitzt, wird als Ruhemasse bezeichnet. Sie kann berechnet werden mit der Gleichung:
$\begin{array}{l} E_{0} = m_{0} \cdot c^{2} \\ E_{0} Ruheenergie \\ m_{0} Ruhemasse \\ c Lichtgeschwindigkeit \end{array}$
Bezogen ist diese Aussage auf ein Inertialsystem, in dem der Körper ruht.

Ein bewegter Körper verändert aus relativistischer Sicht mit der Geschwindigkeit seine Masse und damit auch seine kinetische Energie. Der Energiezuwachs aufgrund der Bewegung beträgt:

$Δ E = Δ m \cdot c^{2} = (m - m_{0}) \cdot c^{2}$

Die Masse m ist dabei die relativistische Masse. Der genannte Term ist zugleich die relativistische kinetische Energie, für die man auch schreiben kann:

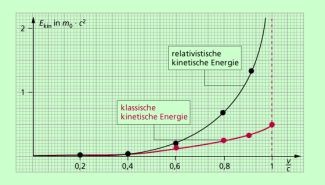
$E_{kin} = (m - m_{0}) \cdot c^{2} = m_{0} \cdot c^{2} (\frac{1}{\sqrt{1 - v^{2} / c^{2}}} - 1)$

Für v = 0 ist die kinetische Energie null. Für kleine Geschwindigkeiten kann die kinetische Energie vernachlässigt werden. Mit Annäherung an die Lichtgeschwindigkeit wird die relativistische kinetische Energie unendlich groß (Bild 2).

Die Gesamtenergie eines Körpers setzt sich aus seiner Ruheenergie und seiner relativistischen kinetischen Energie zusammen. Für die Gesamtenergie gilt:

$\begin{array}{l} E = E_{0} + E_{kin} = \frac{m_{0}}{\sqrt{1 - v^{2} / c^{2}}} \cdot c^{2} \\ E_{0} Ruheenergie \\ E_{kin} relativistische kinetische Energie \\ m_{0} Ruhemasse \\ v Geschwindigkeit in einem Inertialsystem \\ c Lichtgeschwindigkeit \end{array}$

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Ruheenergie und Gesamtenergie

Energie in der klassischen Physik

Energie aus relativistischer Sicht

Rechtliches

Einloggen