Zeitdilatation

In der klassischen Physik wird von einer absoluten Zeit ausgegangen, die überall gleichmäßig verläuft. In der speziellen Relativitätstheorie dagegen ist der Zeitbegriff zu relativieren. Die Zeit ist nicht absolut, sondern es gilt vielmehr: Eine bewegte Uhr geht langsamer als eine ruhende Uhr. Ein physikalischer Vorgang dauert in seinem Ruhesystem nicht so lange wie der gleiche Vorgang in einem dazu bewegten System. Diese Erscheinung wird als Zeitdilatation bezeichnet.

Die Zeit hängt vom jeweiligen Bezugssystem ab. Man spricht deshalb auch von der Relativität der Zeitmessung.

Was bedeutet Relativität der Zeitmessung?

Die Relativität der Gleichzeitigkeit ist mit der Vorstellung einer absoluten Zeit nicht vereinbar. Damit entsteht die Frage, wovon die Zeitdauer eines Vorganges in einem Inertialsystem abhängig ist und ob man für den gleichen Vorgang in einem dazu bewegten Inertialsystem die gleiche Zeitdauer oder eine andere misst.

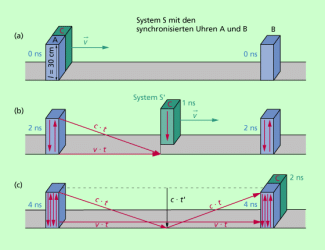
Die Zusammenhänge lassen sich mithilfe eines Gedankenexperiment s verdeutlichen. Wir betrachten dazu ein Inertialsystem S, in dem sich zwei synchronisierte Lichtuhren befinden (Bild 2). Es ist üblich, ein solches System als Ruhesystem zu bezeichnen. Es zeichnet sich allerdings gegenüber anderen System nur durch das Vorhandensein von mindestens zwei synchronisierten Uhren aus.
In einem dazu bewegten System S' befindet sich eine Lichtuhr C, die sich mit der konstanten Geschwindigkeit v an A und B vorbeibewegt.

Dabei gehen wir von folgenden Bedingungen aus:

Wenn sich die Lichtuhr C gerade an A vorbeibewegt, werden die beiden synchronisierten Uhren A und B, aber auch C gestartet.
Während der Bewegung der Uhr C von A nach B läuft das Licht in den Lichtuhren A und B zweimal hin und her.

Analysiert man den Vorgang zunächst aus der Sicht eines Beobachters, der sich ruhend im System S befindet, so ergibt sich:

In den synchronisierten Lichtuhren A und B läuft das Licht während der Bewegung der Uhr C von A nach B zweimal hin und her. Bei einer Länge der Lichtuhren von 30 cm entspricht das einer Zeitdauer von 4 ns.
In der bewegten Lichtuhr C verläuft das Licht schräg und hat einen wesentlich größeren Weg zurückzulegen, für den es wegen der Konstanz der Lichtgeschwindigkeit eine größere Zeit braucht. Das Licht läuft in der Lichtuhr C weniger als zweimal hin und her. Dieser Zusammenhang gilt allgemein und wird als Zeitdilatation oder Zeitdehnung bezeichnet, abgeleitet vom lateinischen dilatare = dehnen.

Eine bewegte Uhr geht langsamer als eine ruhende Uhr. Ein Vorgang in einem bewegten System dauert länger als der gleiche Vorgang in einem Ruhesystem.

Das Ruhesystem ist dabei immer das System, in dem sich zwei synchronisierte Uhren befinden.

Herleitung des quantitativen Zusammenhangs
Der quantitative Zusammenhang lässt sich leicht herleiten, wenn man von Bild 2 ausgeht und auf ein dort markiertes rechtwinkliges Dreieck den Satz des PYTHAGORAS anwendet. Dann erhält man:

(c ⋅ t) ² = (v ⋅ t) ² + (c ⋅ t ') ²

$\begin{array}{l} Die Umstellung dieser Gleichung nach t ergibt die \\ gesuchte Beziehung: \\ c^{2} \cdot t^{2} = v^{2} \cdot t^{2} + c^{2} \cdot t'^{2} \\ c^{2} \cdot t^{2} - v^{2} \cdot t^{2} = c^{2} \cdot t'^{2} \\ t^{2} (c^{2} - v^{2}) = c^{2} \cdot t'^{2} \\ t^{2} = \frac{c^{2} \cdot t'^{2}}{c^{2} - v^{2}} \\ t = \frac{t'}{\sqrt{1 - v^{2} / c^{2}}} = k \cdot t' \end{array}$
Dabei ist t die Zeit im Inertialsystem S (Ruhesystem), t' die im System S', v die Relativgeschwindigkeit und k der LORENTZ-Faktor. Unter den gegebenen Bedingungen gilt immer:
$t > t' und damit auch Δ t > Δ t'$
Das hätte z.B. die Konsequenz, dass Personen, die sich in zueinander bewegten Inertialsystemen befinden, unterschiedlich schnell altern. Berühmt wurde dieses Beispiel unter den Begriffen „ Uhrenparadoxon “ oder „ Zwillingsparadoxon “. Unter dem letzten Stichwort sind auch genauere Erläuterungen dazu zu finden.

Nachfolgend sind einige Beispiele für die Größenordnung der Zeitdilatation genannt.

Objekt	Geschwindigkeit	Prozent der Licht-geschwindigkeit	Faktor der Zeitdehnung
Fußgänger	5 km/h	0,000 000 4	1,000 000 000 000 000 02
Pkw	100 km/h	0,000 009	1,000 000 000 000 004
Düsenjäger	2000 km/h	0,000 002	1,000 000 000 002
Geschosskugel	1 km/s	0,000 003	1,000 000 000 005
Erde um die Sonne	30 km/s	0,000 1	1,000 000 005
Elektronen	100 000 km/s	33	1,059

Herleitung mithilfe der LORENTZ-Transformation
Im System S', das sich gegenüber einem System S mit der Geschwindigkeit v in positiver x-Richtung bewegt, dauert ein physikalischer Vorgang, der in einem bestimmten Punkt x' stattfindet, das Zeitintervall:
$Δ t' = t_{2}' - t_{1}'$
Für einen Beobachter in S dauert der gleiche Vorgang
$Δ t = t_{2} - t_{1}$
Unter Anwendung der LORENTZ-Transformation ergibt sich:

$\begin{array}{l} t_{1} = \frac{t_{1}' + \frac{v}{c^{2}} x}{\sqrt{1 - v^{2} / c^{2}}} t_{2} = \frac{t_{2}' + \frac{v}{c^{2}} x}{\sqrt{1 - v^{2} / c^{2}}} \\ und damit: \\ Δ t = t_{2} - t_{1} = \frac{t_{2}' + \frac{v}{c^{2}} x}{\sqrt{1 - v^{2} / c^{2}}} - \frac{t_{1}' + \frac{v}{c^{2}} x}{\sqrt{1 - v^{2} / c^{2}}} \\ Δ t = \frac{Δ t'}{\sqrt{1 - v^{2} / c^{2}}} \end{array}$

Das ist das gleiche Ergebnis wie oben genannt, hier aber bezogen auf ein Zeitintervall.

Experimentelle Bestätigung der Zeitdilatation

Eine erste experimentelle Bestätigung der Zeitdilatation erfolgte im Oktober 1971 durch die US-amerikanischen Physiker JOSEPH C. HAFELE und RICHARD KEATING. Zum damaligen Zeitpunkt war die Entwicklung von Atomuhren soweit vorangeschritten, dass transportable Atomuhren zur Verfügung standen und damit sehr genaue Zeitmessungen in unterschiedlichen Bezugsystemen möglich wurden.
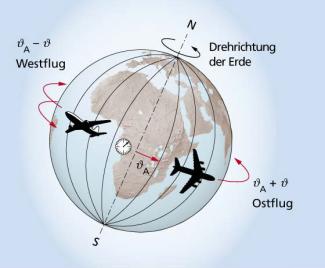
HAFELE und KEATING synchronisierten einige Atomuhren. Eine Uhrengruppe aus vier Atomuhren verblieb auf der Erde. Eine zweite Gruppe umkreiste innerhalb von zwei Tagen in einem Flugzeug die Erde in östlicher Richtung, die dritte in westlicher Richtung (Bild 3). Verglichen wurde dann der Gang der Uhren. Es wurden jeweils mehrere Uhren genutzt, um Mittelwerte bilden zu können.

Ein relativ zur Erde ruhender Beobachter, der nicht an der Erdrotation teilnimmt, würde dann feststellen:

Die Uhr auf der Erde bewegt sich am Äquator mit etwa 40.000 km/h oder 463 m/s.
Die Uhren, die sich im ostwärts fliegenden Flugzeug befinden, bewegen sich mit 40.000 km/h + 800 km/h, also schneller. Die Zeit müsste demzufolge bei diesen Uhren langsamer vergehen.
Die Uhren, die sich im westwärts fliegenden Flugzeug befinden, bewegen sich mit 40.000 km/h - 800 km/h, also langsamer. Die Zeit müsste demzufolge bei diesen Uhren schneller vergehen.

Ergebnis dieses Experiments war: Gegenüber den auf der Erde verbliebenen Atomuhren wurden sowohl beim Flug in östlicher wie auch beim Flug in westlicher Richtung deutliche Zeitdifferenzen festgestellt:
$Δ t_{o s t} = (- 255 \pm 10) ns Δ t_{w e s t} = (+ 77 \pm 7) ns$
Diese experimentellen Daten stimmten im Rahmen der Messgenauigkeit mit den berechneten Daten überein, wobei die Berechnung überaus kompliziert war, weil z.B. der unterschiedliche Gang der Uhren in Abhängigkeit vom Gravitationsfeld (Gravitations-Zeitdilatation) berücksichtigte werden musste und auch zu beachten war, dass sich weder die Atomuhren auf der Erdoberfläche noch die in den Flugzeugen in einem Inertialsystem befanden.
Die Messergebnisse wurden lange angezweifelt. Heute werden sie als erste experimentelle Bestätigung der Zeitdilatation allgemein anerkannt.

Eine weitere experimentelle Bestätigung erfolgte 1985 im Rahmen der D1-Weltraummission, an der die deutschen Astronauten R. FURRER und E. MESSERSCHMID teilnahmen. Hier wurde im Rahmen des NAVEX-Experiments der Gang von Atomuhren auf der Erde und in einem Raumschiff miteinander verglichen. Das Navigationsexperiment NAVEX diente vor allem dem Test von Sychronisationstechniken für Atomuhren in Satelliten und Bodenstationen und war damit ein wichtiger Schritt zur satellitengestützten Navigation (GPS).

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Kostenlos ausprobieren

Verwandte Artikel

Zeitdilatation

Was bedeutet Relativität der Zeitmessung?

Experimentelle Bestätigung der Zeitdilatation

Rechtliches

Einloggen