Äquivalenz von Masse und Energie

Historisches zu Masse und Energie

Masse und Energie (früher auch häufig als Kraft bezeichnet) waren in der klassischen Physik Größen, die unabhängig voneinander existierten und lediglich bei einigen Gleichungen, z.B. bei den Gleichungen für die potenzielle oder kinetische Energie, beide eine Rolle spielten. Das änderte aber nichts an ihrer voneinander unabhängigen Existenz.
Neben einem Energieerhaltungssatz gab es auch einen Satz von der Erhaltung der Masse. Beide gelten im Bereich der klassischen Physik.
Bestimmten Objekten wurde nur eine Energie; ABER KEINE Masse zugeordnet, z.B. dem Licht oder dem elektrischen Feld. Ende des 19. Jahrhunderts waren aber auch einige Erscheinungen und experimentelle Ergebnisse bekannt, die im Rahmen der klassischen Theorie nicht befriedigend erklärt werden konnten. Dazu gehörten z.B. der von HALLWACHS entdeckte lichtelektrische Effekt, die von BECQUEREL entdeckte radioaktive Strahlung oder die Ergebnisse der Experimente von MICHELSON und MORLEY zum Äther.

Eine neue Sicht auf Masse und Energie

Mit seinen 1905 veröffentlichten Arbeiten zur speziellen Relativitätstheorie entwickelte ALBERT EINSTEIN (1879-1955) nicht nur neue Vorstellungen über Raum und Zeit. In seinem 1905 erschienenen Beitrag unter dem Titel „Ist die Trägheit eines Körpers von seinem Energiegehalt abhängig?“ stellte EINSTEIN fest:

„Die Masse eines Körpers ist ein Maß für dessen Energiegehalt“.

Den quantitativen Zusammenhang zwischen Masse und Energie gab er in Form einer Gleichung an, die sicher zu den berühmtesten und bekanntesten Gleichungen der Physik gehört. Sie lautet:

$\begin{array}{l}E=m\cdot c^2\\ E\text{Gesamtenergie eines Körpers}\\ m\text{dynamische (relativistische) Masse des Körpers}\\ c\text{Lichtgeschwindigkeit}\end{array}$
In Worten: Die Gesamtenergie eines Körpers und seine dynamische Masse sind zueinander proportional. Masse und Energie sind äquivalent. Man spricht auch vom Äquivalenzprinzip.

Was bedeutet Äquivalenz von Masse und Energie?

Äquivalenz von Masse und Energie bedeutet im Unterschied zur Auffassung der klassischen Physik, dass die beiden Größen nicht unabhängig voneinander existieren, sondern dass jeder Form von Energie eine Masse zugeordnet werden kann und umgekehrt jeder Masse eine Energie entspricht.
Äquivalenz bedeutet auch:

Jede Masseänderung bedeutet eine Energieänderung und umgekehrt.

Es bedeutet darüber hinaus:

• In jedem abgeschlossenen System ist die Erhaltung der Energie gleichbedeutend mit der Erhaltung der Masse. In relativistischer Betrachtungsweise umfasst der allgemeine Energieerhaltungssatz den Satz von der Erhaltung der Masse.
• Der Zusammenhang zwischen Energie und Masse ist nicht auf mechanische Vorgänge beschränkt, sondern gilt für beliebige Vorgänge in der Makrophysik und in der Mikrophysik, also z.B. für die Sonne ebenso wie für die Entstehung von Strahlung bei Zerfall eines Elektron-Positron-Paares (Paarzerstrahlung), für die Spaltung eines Urankerns ebenso wie beim Erwärmen von Wasser durch Energiezufuhr.
• Einer Veränderung der Masse entspricht eine bestimmte Energie. Die Verringerung der Masse wird in der Physik als Massendefekt bezeichnet. Für den Zusammenhang zwischen der Veränderung der Masse und der Energie gilt: $E=\Delta m\cdot c^2$
• Objekten, die keine Ruhemasse haben (z.B. Photonen, Neutrinos), kann aufgrund der Äquivalenz von Energie und Masse eine Masse zugeordnet werden, die man auch als Impulsmasse oder Ersatzmasse bezeichnet. Diese Impulsmasse ergibt sich aus der Beziehung: $m=\frac{E}{c^2}$

Beispiele für die Äquivalenz vom Masse und Energie

Der grundlegenden Zusammenhang von Masse und Energie spielt bei vielen Vorgängen in der Atom- und Kernphysik sowie in der Physik der Elementarteilchen eine fundamentale Rolle. Auch bei Alltagsvorgängen gibt es diesen Zusammenhang zwischen Masse und Energie. Die dabei auftretenden Effekte sind aber so gering, dass sie völlig vernachlässigt werden können. Völlig anders ist das z.B. in der Kernphysik (siehe Beispiele).

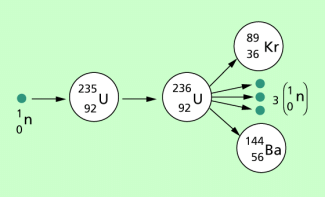
Beispiel 1: Kernspaltung

Kernspaltung bedeutet, dass Atomkerne von Elementen spontan oder durch äußere Beeinflussung in Kerne leichterer Elemente zerfallen und dabei Energie freigesetzt wird. Nach der Äquivalenz von Energie und Masse entspricht einer Energiefreisetzung eine Verringerung der Masse. So erfolgt beispielsweise die Spaltung von Uran-235 entsprechend der Gleichung:
${}_{92}{}^{235}\text{U}+{}_0{}^1\text{n}\to {}_{56}{}^{143}\text{B}\text{a}+{}_{36}{}^{90}\text{K}\text{r}+3\cdot \left({}_0{}^1\text{n}\right)+\Delta E$

Aus dieser Reaktionsgleichung folgt die Massebilanz bei der Kernspaltung:

$\begin{array}{l}\text{vor der Spaltung:}\\ {}_{\text{92}}{}^{\text{235}}\text{U}\text{: 235}\text{,0439}u\\ {}_{\text{0}}{}^{\text{1}}\text{n}\text{: 1}\text{,00898}u\\ \text{\_\_\_\_\_\_\_\_\_\_\_}\\ \text{236}\text{,0529}u\\ \\ \text{nach der Spaltung:}\\ {}_{\text{56}}{}^{143}\text{B}\text{a: 142}\text{,9084}u\\ {}_{\text{36}}{}^{\text{90}}\text{K}\text{r: 89}\text{,9043}u\\ 3\cdot \left({}_{\text{0}}{}^{\text{1}}\text{n}\right):\text{3}\text{,0296}u\\ \text{\_\_\_\_\_\_\_\_\_\_}\\ \text{235}\text{,8396}u\\ \Delta m=\mathrm{0,2133}u\\ \end{array}$
Diesem Massendefekt entspricht eine Energie, die bei der Kernspaltung freigesetzt wird:
$\begin{array}{l}E=\Delta m\cdot c^2\\ E=\mathrm{0,21833}\cdot \mathrm{1,661}\cdot {10}^{-27}\text{kg}\cdot {\left(\mathrm{2,99}792\cdot {10}^8\frac{\text{m}}{\text{s}}\right)}^2\\ E=\mathrm{3,18}\cdot {10}^{-11}\text{J}\\ E=198\text{MeV}\end{array}$

Das bedeutet: Bei der Kernspaltung ist die Masse vor der Spaltung größer als nach der Spaltung. Dem Massendefekt entspricht bei der Spaltung eines Urankerns eine Energie von ca. 200 MeV.

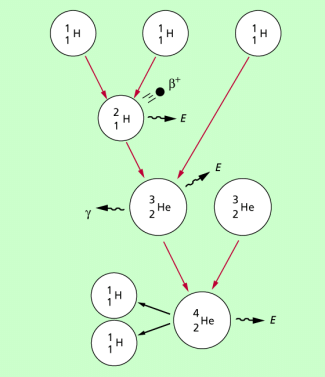
Beispiel 2: Kernfusion

Kernfusion im Inneren der Sonne ist die Quelle der Sonnenenergie, die Voraussetzung für die Entstehung und Entwicklung des Lebens auf der Erde ist. In jeder Sekunde verschmelzen im Inneren der Sonne 567 Mio. Tonnen Wasserstoff zu 562,8 Mio. Tonnen Helium (Bild 3). Der Massendefekt beträgt damit in jeder Sekunde 4,2 Mio. Tonnen. Daraus ergibt sich die Energie, die in jeder Sekunde von der Sonne abgegeben wird:
$\begin{array}{l}E=\Delta m\cdot c^2\\ E=\mathrm{4,2}\cdot {10}^9\text{kg}\cdot {\left(\mathrm{2,99792}\cdot {10}^8\frac{\text{m}}{\text{s}}\right)}^2\\ E=\mathrm{3,8}\cdot {10}^{26}\text{J}\end{array}$

Das entspricht einer Strahlungsleistung der Sonne (in der Astronomie als Leuchtkraft L bezeichnet) von: $L=\mathrm{3,8}\cdot {10}^{26}\text{W}$

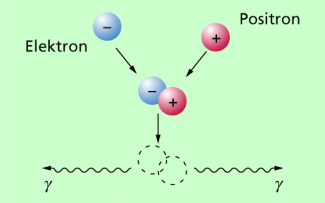
Beispiel 3: Paarzerstrahlung

Die 1932 von ANDERSON entdeckten Positronen treten mit Elektronen in Wechselwirkung. Dabei tritt ein Effekt auf, der als Paarzerstrahlung oder Paarvernichtung bezeichnet wird: Ein Elektron-Positron-Paar verschwindet, dabei entsteht Gammastrahlung (Bild 4).
Damit ergibt sich für diese Paarzerstrahlung die folgende Bilanz:

$\begin{array}{l}\text{1 Elektron + 1 Positron}\to \text{2}\gamma \text{-Quanten}\\ \text{Massenbilanz: 9}\text{,1}\cdot {\text{10}}^{\text{-31}}\text{kg + 9}\text{,1}\cdot {\text{10}}^{\text{-31}}\text{kg = 18}\text{,2}\cdot {\text{10}}^{\text{-31}}\text{kg}\\ \text{Energiebilanz: 0}\text{,51 MeV + 0}\text{,51 MeV = 1}\text{,02 MeV}\end{array}$

Beispiel 4: Paarbildung

Auch der umgekehrte Vorgang, die Paarbildung, ist möglich. Die wichtigste Paarbildung ist die Umwandlung eines Photons in ein Elektron-Positron-Paar.
Dazu ist eine Mindestenergie des Photons von 1,02 MeV erforderlich, denn es muss entsprechend der Äquivalenz von Energie und Masse mindestens die Energie vorhanden sein, die der Masse eines Elektrons plus eines Positrons äquivalent ist.
Die Paarbildung spielt eine entscheidende Rolle bei der Schwächung elektromagnetischer Strahlung beim Durchgang durch Stoffe. Insbesondere gilt das auch für die Strahlung, die aus dem Weltraum auf die Erdatmosphäre trifft: Durch Paarbildung in der Erdatmosphäre wird die auftreffende Strahlung erheblich abgeschwächt.

Beispiel 5: Kernbindungsenergie

Als Kernbindungsenergie wird die Energie bezeichnet, die erforderlich wäre, um einen Kern in seine Bestandteile zu zerlegen. Es ist zugleich die Energie, die frei wird, wenn ein Kern aus seinen Bestandteilen zusammengefügt wird.
Dabei gilt: Die Masse der Bestandteile eines Kerns ist größer als die Kernmasse. Beim Zusammenfügen der Bestandteile tritt ein Massendefekt auf, der der Kernbindungsenergie äquivalent ist. Es gilt:

$\begin{array}{l}{E}_{\text{B}}=(Z\cdot m_{\text{P}}+N\cdot m_{\text{N}}-m_{\text{K}})\cdot c^2\\ E_{\text{B}}\text{Kernbindungsenergie}\\ Z\text{Anzahl der Protonen im Kern}\\ m_{\text{P}}\text{Masse eines Protons}\\ N\text{Anzahl der Neutronen im Kern}\\ m_{\text{P}}\text{Masse eines Neutrons}\\ m_{\text{K}}\text{Masse des Atomkerns}\\ c\text{Lichtgeschwindigkeit}\end{array}$

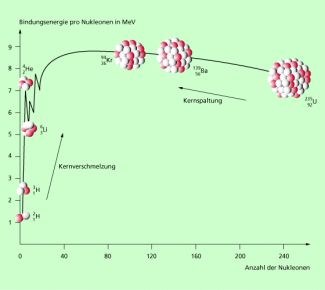
Damit kann man für einzelne Atomkerne die Kernbindungsenergie berechnen. Die Kernbindungsenergie hängt von der Nukleonenzahl ab (Bild 5). Die mittlere Bildungsenergie je Nukleon liegt zwischen 7 MeV und 9 MeV.