MINKOWSKI-Diagramme
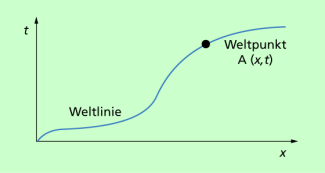
MINKOWSKI-Diagramme, auch Raum-Zeit-Diagramme genannt, sind von dem deutschen Mathematiker HERMANN MINKOWSKI (1864-1909) entwickelte Diagramme zur anschaulichen Beschreibung der Bewegung eines Körpers (Massepunktes) in Raum und Zeit. Bei der Bewegung eines Massepunktes entsteht im Diagramm eine Linie (Weltlinie), wobei jeder Punkt der Weltlinie einem bestimmten Ort und einem bestimmten Zeitpunkt entspricht. Ein solcher Punkt wird als Weltpunkt bezeichnet.
MINKOWSKI hat diese Art von Diagrammen bei der von ihm vorgenommenen mathematischen Ausgestaltung der speziellen Relativitätstheorie von ALBERT EINSTEIN entwickelt. Er formulierte 1908:
„Raum und Zeit haben ihre Selbständigkeit verloren. Sie sinken zu Schatten herab und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.“
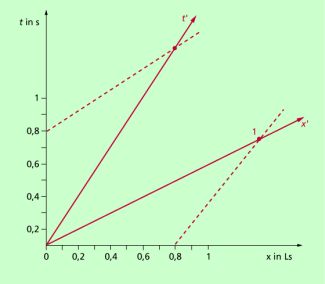
Ausdruck für diese Position sind die MINKOWSKI-Diagramme. Bild 1 zeigt eine Variante: Dargestellt ist eine Weltlinie in einem x-t-Diagramm. Die Beschränkung auf eine Koordinate (x) und die Zeit (t) macht die Diagramme besonders gut überschaubar. Eigentlich erfordert eine allgemeine Darstellung ein vierdimensionales Koordinatensystem mit drei Raumkoordinaten x, y, z und einer Zeitkoordinate t. Diese vierdimensionale Raum-Zeit wird auch als MINKOWSKI-Welt bezeichnet. Legt man die Raumachse in Bewegungsrichtung und bezeichnet man diese mit x, dann ändern sich y und z nicht und man kann die räumliche Bewegung in einem x-t-Diagramm darstellen.
-
Weltlinie und Weltpunkt für die Bewegung eines Massepunktes, dargestellt in einem Raum-Zeit-Diagramm (MINKOWSKI-Diagramm)
Aufbau von MINKOWSKI-Diagrammen
Arbeitet man mit MINKOWSKI-Diagrammen, dann ist es zweckmäßig, sich an die allgemein üblichen Vereinbarungen für diese Diagramme zu halten. Diese Vereinbarungen sind aus Gründen der Zweckmäßigkeit getroffen:
- Als Einheit für die Zeitachse t wird die Sekunde verwendet.
- Als Einheit der Ortsachse x wird die Länge der Strecke genutzt, die Licht im Vakuum in einer Sekunde zurücklegt:
Diese Strecke wird als eine Lichtsekunde (1 Ls) bezeichnet. Damit gilt: 1 Ls = 300 000 km
- Bei der Achseneinteilung werden auf beiden Achsen stets die gleichen Strecken für eine Einheit abgetragen, z.B.:
Bei der t-Achse entspricht einer Sekunde eine Strecke von 2 cm.
Bei der x-Achse entspricht einer Lichtsekunde ebenfalls eine Strecke von 2 cm.
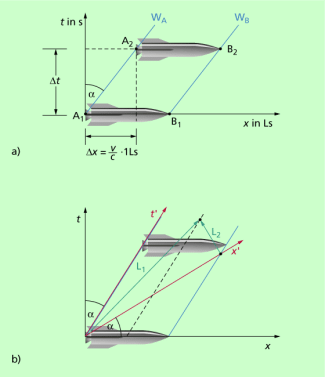
Mit diesen Vereinbarungen verlaufen die Weltlinien von Lichtsignalen immer parallel zu der Winkelhalbierenden der Achsen, im rechtwinkligen Koordinatensystem also unter einem Winkel von 45° zur x-Achse und damit auch zur t-Achse. Eine Bewegung in Richtung positiver x-Achse bedeutet eine Verschiebung nach rechts (Bild 2).
Die Weltlinien für die Punkte A und B sind bei gleichförmiger Relativbewegung Geraden. Der Winkel wird durch die Geschwindigkeit v festgelegt (siehe Bild 2a) und beträgt bei Lichtsignalen 45°. Dieser Wert kann nicht überschritten werden, da die Lichtgeschwindigkeit die größtmögliche Geschwindigkeit ist.
Von einem als ruhend angenommenen System S aus betrachtet bewegt sich die Rakete nach rechts (Bild 2a). Vom mit der Rakete verbundenen System S' aus ergibt sich das in Bild 2b rot dargestellte Diagramm: S' bewegt sich gegenüber S mit der Geschwindigkeit v nach rechts. Die t'-Achse verläuft damit parallel zu den Weltlinien der Punkte A und B. Ihre Richtung ergibt sich also wie die der Weltlinien (siehe oben).
Die Richtung der x'-Achse ergibt sich aus dem Winkel . Dieser Winkel tritt nicht nur zwischen t und t', sondern auch zwischen x und x' auf (Bild 2b). Inhaltlich ergibt sich die Richtung von x' auch durch folgende Überlegung: Von der Spitze und vom Ende der Rakete (siehe Bild 2b) werden Lichtsignale so ausgesendet, dass sie gleichzeitig in der geometrischen Mitte der Rakete eintreffen. Die Weltlinien der Lichtsignale sind wegen der Konstanz der Lichtgeschwindigkeit in beiden Systemen Winkelhalbierende. Damit ergibt sich die Richtung von x'.
Im System S' mit (t',x') ergibt sich die Längeneinheit e' für die Achseneinteilung aus der entsprechenden Längeneinheit e im System S mit folgender Gleichung:
Beträgt also z.B. in S die Längeneinheit für die Achseneinteilung e = 2 cm und die Relativgeschwindigkeit zwischen den Systemen v = 0,6 c, so erhält man für e':
Das gilt für beide Achsen. Die Einheitenstrecken sind also auf den gedrehten Achsen stets größer als auf der senkrechten und waagerechten Achse.
Eine grafische Möglichkeit für die Festlegung der Einheiten ist im Beispiel 1 bei den Anwendungen (siehe unten) gegeben.
-
Bewegung eines Körpers in Raum und Zeit, dargestellt in MINKOWSKI-Diagrammen für einen ruhenden Beobachter (a) und für einen mitbewegten Beobachter (b)
Was kann man im MINKOWSKI-Diagramm anschaulich darstellen?
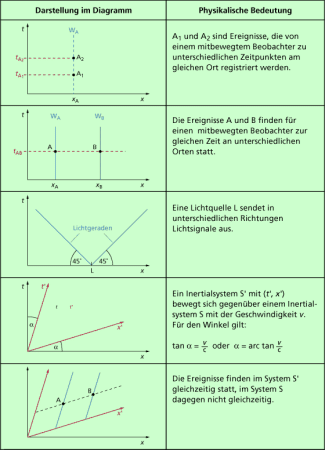
In der nebenstehenden Übersicht (Bild 3) sind charakteristische Weltlinien und ihre physikalische Bedeutung in übersichtlicher Form zusammengestellt. Diese Zusammenstellung ist sehr hilfreich für das Verständnis der Anwendungen, die nachfolgend erläutert sind.
-
Bedeutung ausgewählter Linien in MINKOWSKI-Diagrammen
Beispiele für die Anwendung von MINKOWSKI-Diagrammen
Nachfolgend sind einige ausgewählte Beispiele für die Anwendung von Minkowski-Diagrammen zusammengestellt und erläutert.
Beispiel 1: Bestimmung der Einheiten auf den Achsen
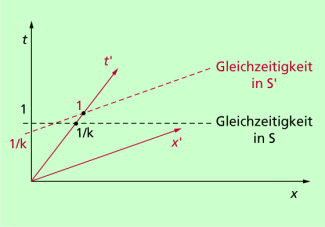
Betrachtet werden zwei Inertialsysteme S und S', wobei sich S' mit einer Geschwindigkeit von 0,6 c in x-Richtung bewegt. Dann kann man nach Festlegung der Einheiten in S die in S' so festlegen, wie es in Bild 4 dargestellt ist:
- Berechnet wird zunächst der Faktor 1/k (Kehrwert des LORENTZ-Faktors):
- Die Parallele zur x'-Achse durch den Wert 1/k = 0,8 der t-Achse ergibt die Einheit 1 auf der t'-Achse.
- Die Parallele zur t'-Achse durch den Wert 1/k = 0,8 der x-Achse ergibt die Einheit 1 auf der x'-Achse.
Ist eine Achseneinteilung vorhanden, so können mithilfe von MINKOWSKI-Diagrammen auch quantitative Aussagen gemacht werden.
-
Grafische Bestimmung der Einheiten auf den Achsen eines t'-x'-Diagramms, wenn die Einheiten beim t-x-Diagramm festgelegt sind.
Beispiel 2: Ankunft von Lichtsignalen
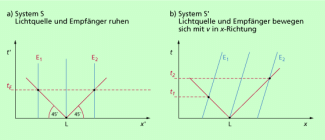
Bei zwei von einer Lichtquelle gleich weit entfernten Empfängern soll ein von der Lichtquelle ausgesandtes Lichtsignal gleichzeitig ankommen. Auf diese Weise werden z.B. Lichtuhren synchronisiert (EINSTEIN-Synchronisation).
In Bild 5 ist dieser Vorgang in einem System S' dargestellt, in dem sich die Lichtquelle und die Empfänger in Ruhe befinden. Das Licht trifft gleichzeitig bei den beiden Empfängern ein (Bild 5a).
Bewegt sich S' gegenüber S mit größerer Geschwindigkeit in x-Richtung, so stellt sich für einen Beobachter in S der Sachverhalt anders dar (Bild 5b): Den Empfänger 1 erreicht das Lichtsignal eher als den Empfänger 2.
-
Ankunft eines Lichtsignals bei zwei Empfängern, dargestellt in verschiedenen Inertialsystemen.
Beispiel 3: Zeitdilatation
Zeitdilatation bedeutet, dass bewegte Uhren langsamer gehen als ruhende Uhren. Bild 6 zeigt den Sachverhalt für ein ruhendes System S und ein dazu bewegtes System S'.
Wenn man sich im System S befindet und dort eine Zeiteinheit vergangen ist, dann sind im System S' genau 1/k Zeiteinheiten vergangen. k ist der LORENTZ-Faktor mit k > 1.
Umgekehrt gilt: Wenn man sich im System S' befindet und dort eine Zeiteinheit vergangen ist, sind es im System S dann 1/k Zeiteinheiten.
-
Darstellung der Zeitdilatation im MINKOWSKI-Diagramm