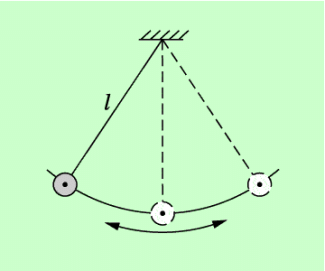
Fadenpendel
Beispiele für schwingende Körper, die man vereinfacht als Fadenpendel betrachten kann, sind eine Kinderschaukel, das Pendel einer Uhr oder ein Artist am Trapez.
Schwingungsdauer und Frequenz eines Fadenpendels
Die Schwingungsdauer (Periodendauer) eines Fadenpendels hängt von seiner Länge und dem Ort ab, an dem es sich befindet. Sie ist umso größer, je größer die Länge des Pendels ist.
Unter der Bedingung kleiner Auslenkungen gilt:
Beachte:
- Die Länge des Pendels ist der Abstand zwischen dem Aufhängepunkt und dem Schwerpunkt des schwingenden Körpers (Pendelkörpers).
- Die Fallbeschleunigung g ändert sich mit dem Ort. Ihr mittlerer Wert auf der Erdoberfläche beträgt
- Die Masse des Pendelkörpers hat keinen Einfluss auf die Schwingungsdauer.
Da zwischen der Schwingungsdauer und der Frequenz der Zusammenhang
besteht, erhält man für die Frequenz eines Fadenpendels die Gleichung:
Ein Fadenpendel führt näherungsweise harmonische Schwingungen aus.
Material zum Thema
Kennzeichnung der Schwingung eines Fadenpendels
Bei kleinen Auslenkungen führt ein Fadenpendel harmonische Schwingungen oder sinusförmige Schwingungen aus.
Wird es nur einmal ausgelenkt, so verringert sich allmählich infolge des Luftwiderstandes und anderer Reibungseffekte die Amplitude. Es liegt eine gedämpfte Schwingung vor.
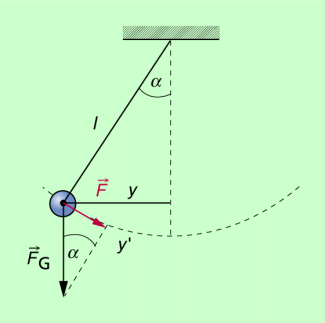
Bei einem Fadenpendel wird ständig potenzielle in kinetische Energie umgewandelt und umgekehrt (Bild 2). Durch Reibung verringert sich die mechanische Energie allmählich.
Die rücktreibenden Kräfte sind jeweils Komponenten der Gewichtskraft, die tangential zur Bahnkurve in Richtung Ruhelage wirken.
Für die tangential gerichtete Komponente der Gewichtskraft, die rücktreibende Kraft, gilt:
Die genannte Gleichung gilt nur unter folgenden Bedingungen:
- Der Pendelkörper kann als Massepunkt angesehen werden.
- Die Masse des Fadens kann vernachlässigt werden.
- Die Auslenkung ist so klein, dass
gesetzt werden kann, also der Kreisbogen näherungsweise gleich der linearen Auslenkung ist (Bild 2).
Das ist dann der Fall, wenn ist.
Vergleicht man die Werte genauer, dann ergibt sich:
| Abweichung in Prozent | |||
| 5° | 0,08727 | 0,08716 | 0,13 % |
| 10° | 0,1745 | 0,1736 | 0,52 % |
| 15° | 0,2618 | 0,2588 | 1,15 % |
| 20° | 0,3491 | 0,3420 | 2,03 % |
| 25° | 0,4363 | 0,4226 | 3,14 % |
| 30° | 0,5236 | 0,5000 | 4,51 % |
Im Rahmen einer sinnvollen Genauigkeit kann man die Schwingungen eines Fadenpendels bis zu einem Auslenkungswinkel von etwa 25° als harmonische Schwingungen ansehen.
Die rücktreibende Kraft bei einem Fadenpendel ist eine Komponente der Gewichtskraft.
Der Pendelversuch von Foucault
Der französische Physiker JEAN BERNARD LEON FOUCAULT (1819-1868) entwickelte um 1850 eine Experimentieranordnung zum unmittelbaren Nachweis der Rotation der Erde. Dazu befestigte er nach anfänglichen Versuchen in der Pariser Sternwarte in der Kuppel des Pantheon in Paris ein 67 m langes Pendel mit einem 28 kg schweren Pendelkörper (Bild 3). Unter der Pendelspitze wurde auf dem Fußboden eine Markierung angebracht. Da ein Pendel seine Schwingungsebene im Raum beibehält, dreht sich infolge der Rotation der Erde die Markierung allmählich gegenüber der Pendelebene. Diese Drehung konnte man bereits nach wenigen Minuten beobachten. Am Pol beträgt sie in 24 Stunden 360° und damit in einer Minute 0,25°. Auf einer mittleren geografischen Breite von 50° (Berlin, Paris) sind es etwa 0,2° in jeder Minute.
Diese Drehung ist ein Beweis dafür, dass die Erde um ihre Achse rotiert. Ein solches Pendel, mit dem man die Erdrotation nachweisen kann, bezeichnet man als foucaultsches Pendel.
Foucaultscher Pendelversuch im Pantheon in Paris
Rotation der Erde Berechnung foucaultsches Pendel rücktreibende Kräfte harmonische Schwingung Frequenz Jean Bernard Léon Foucault sinusförmige Schwingung Periodendauer Simulation Rechenbeispiel gedämpfte Schwingung Schwingungsdauer mechanischer Schwinger
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 