Geschwindigkeitsverteilung von Teilchen

Gegenstand der kinetischen Gastheorie ist die Betrachtung thermodynamischer Prozesse auf der Grundlage von Teilchengrößen, wie der Teilchenanzahl, ihrer räumlichen Verteilung und ihrer Energie. Von besonderer Bedeutung ist die Geschwindigkeitsverteilung der Teilchen eines Gases, da die Geschwindigkeit eng mit der kinetischen Energie, dem Druck und auch mit der Temperatur verknüpft ist. Untersuchungen zeigen, dass zwischen der mittleren Geschwindigkeit, der wahrscheinlichsten Geschwindigkeit und der mittleren quadratischen Geschwindigkeit der Teilchen unterschieden werden muss.

Teilchenmodell

#Teilchenmodell #Atome #Aggregatzustände #Wechselwirkungen

Beschleunigung berechnen

#Bewegung #Geschwindigkeit #Beschleunigung #Weg-Zeit-Diagramm

Geschwindigkeitsverteilung von Teilchen

Gegenstand der kinetischen Gastheorie ist die Betrachtung thermodynamischer Prozesse auf der Grundlage von Teilchengrößen, wie der Teilchenanzahl, ihrer räumlichen Verteilung und ihrer Energie. Von besonderer Bedeutung ist die Geschwindigkeitsverteilung der Teilchen eines Gases, da die Teilchengeschwindigkeit eng mit der kinetischen Energie und auch mit der Temperatur verknüpft ist.

Verlauf der Geschwindigkeitsverteilung
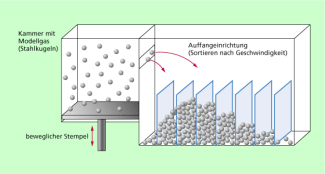
Die Verteilung der Geschwindigkeit von Teilchen in einem Gas kann anhand eines Modellgases (des idealen Gases) untersucht werden. Experimentell lässt sich das so realisieren, dass man in einem Schüttelapparat kleine Stahlkugeln zu schnellen Bewegungen anregt, die Teilchen an einer bestimmten Stelle die Apparatur verlassen können und Teilchen gleicher Geschwindigkeit jeweils gesammelt werden (Bild 2). Führt man dieses Experiment mit einer hinreichend großen Anzahl von Teilchen durch und macht die Sortierung nach Geschwindigkeiten ausreichend fein, so erhält man eine charakteristische Geschwindigkeitsverteilung, die in der Auffangvorrichtung angedeutet ist (Bild 2).

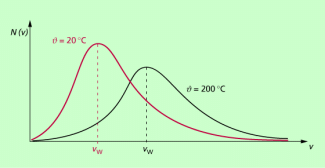
Genauere Untersuchungen ergeben charakteristische Kurven, so wie sie in Bild 3 dargestellt sind. Dabei zeigt sich:

Die Teilchen eines Gases haben unterschiedliche Geschwindigkeiten.
Die Geschwindigkeitsverteilung ist temperaturabhängig.
Insbesondere wird aus dem Diagramm erkennbar, dass die Geschwindigkeitsverteilung nicht symmetrisch ist, sondern gilt: Es gibt ein deutlich ausgeprägtes Maximum der Geschwindigkeit (Spitze des Graphen), um das herum die meisten Teilchen liegen. Diese Geschwindigkeit wird als wahrscheinlichste Geschwindigkeit $v_{w}$ bezeichnet.
Die Anzahl der Teilchen mit höherer Geschwindigkeit ist größer als die mit kleinerer Geschwindigkeit.

Die beschriebene Geschwindigkeitsverteilung leitete der britische Physiker JAMES CLERK MAXWELL (1831-1879) um 1860 unter Nutzung der Wahrscheinlichkeitstheorie her. Sie wird deshalb auch als maxwellsche Geschwindigkeitsverteilung bezeichnet. Die Gleichung für die Kurve lautet:
$\begin{array}{l} N (v) = \frac{4 v^{2}}{\sqrt{π}} {(\frac{1}{2 R_{s} \cdot T})}^{3 / 2} \cdot e^{(- \frac{v^{2}}{2 R_{s} \cdot T})} d v \\ N (v) Anteil der Teilchen mit einer Geschwindigkeit \\ im Intervall [v, v + d v] \\ v Geschwindigkeit \\ R_{s} spezifische Gaskonstante \\ T absolute Temperatur \end{array}$

Material zum Thema

BWS-PHY2-0299-07.htm

BWS-PHY2-0299-07.htm

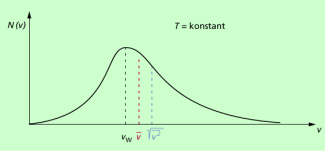
In Bild 4 sind die verschiedenen Geschwindigkeiten dargestellt:

Die wahrscheinlichste Geschwindigkeit $v_{w}$ entspricht dem Kurvenmaximum.
Aufgrund des unsymmetrischen Kurvenverlaufs ist die mittlere Geschwindigkeit $\bar{v}$ größer als die wahrscheinlichste Geschwindigkeit.
Für statistische Betrachtungen ist darüber hinaus der quadratische Mittelwert der Geschwindigkeit, auch mittleres Geschwindigkeitsquadrat $\sqrt{\bar{v^{2}}}$ genannt, von Bedeutung.

Diese drei Geschwindigkeiten kann man folgendermaßen berechnen:

$\begin{array}{l} v_{w} = \sqrt{2 R_{s} \cdot T} = \sqrt{\frac{2 R \cdot T}{M}} \\ \bar{v} = \sqrt{\frac{8 R_{s} \cdot T}{π}} = \sqrt{\frac{8 R \cdot T}{π \cdot M}} \\ \sqrt{\bar{v^{2}}} = \sqrt{3 R_{s} \cdot T} = \sqrt{\frac{3 R \cdot T}{M}} \end{array}$

Damit ergibt sich für das Verhältnis der drei Geschwindigkeiten zueinander:

$\begin{array}{l} v_{w} : \bar{v} : \sqrt{\bar{v^{2}}} = 1 : 1,128 : 1,225 \\ Für die einzelnen Zusammenhänge erhält man: \\ v_{w} = \frac{\sqrt{π}}{2} \bar{v} \approx 0,886 \bar{v} \\ v_{w} = \sqrt{\frac{2}{3}} \sqrt{\bar{v^{2}}} \approx 0,816 \sqrt{\bar{v^{2}}} \\ \bar{v} = \sqrt{\frac{8}{3 π}} \cdot \sqrt{\bar{v^{2}}} \approx 0,921 \sqrt{\bar{v^{2}}} \end{array}$
Ermittelt man die Geschwindigkeiten für verschiedene Gase bei Normbedingungen, so erhält man Geschwindigkeiten in der Größenordnung zwischen 300 m/s und 500 m/s.

Der Versuch von STERN

Dem deutschen Physiker OTTO STERN (1880-1969) gelang 1920 erstmals der Nachweis, dass die Geschwindigkeit von Molekülen mit der berechneten Geschwindigkeit übereinstimmt. Das Experiment nennt man deshalb Versuch von STERN. STERN erhielt für seine Beiträge zur Entwicklung der Molekularstrahlmethode und die Entdeckung des magnetischen Moments des Protons 1943 den Nobelpreis für Physik.
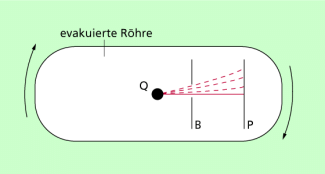
Bild 5 zeigt den prinzipiellen Versuchsaufbau. In einem evakuierten Gefäß befindet sich eine Molekülquelle. O. STERN nutzte dazu einen elektrisch erhitzten, mit Silber überzogenen Platindraht. Von der Quelle aus bewegen sich die Moleküle mit einer mittleren Geschwindigkeit in den Raum hinaus. Durch Blenden B wird ein kegelförmiges Bündel von Molekülen ausgeblendet, die sich auf der Glasplatte P niederschlagen können. Wird die ganze Apparatur in rasche Umdrehungen versetzt, wobei die Drehachse senkrecht zu den Molekularstrahlen (senkrecht zur Zeichenebene) verläuft, so wird sich der Fleck auf der Auffangplatte etwas entgegen der Drehrichtung verschieben, da die von Q ausgehenden Moleküle eine bestimmte Zeit brauchen, um die Strecke zwischen B und P zu durchfliegen. Je nach ihrer Geschwindigkeit treffen sie an verschiedenen Stellen auf die Platte P. Es kommt also auf der Platte zu einer Intensitätsverteilung der auftreffenen Silbermoleküle. aus dieser Intensitätsverteilung lässt sich die Geschwindigkeitsverteilung berechnen.
Versuche mit verbesserter Anordnung.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Angaben zum Lexikon

Impressum

Geschwindigkeitsverteilung von Teilchen

Teilchenmodell

Beschleunigung berechnen

BWS-PHY2-0299-07.htm

Der Versuch von STERN

Rechtliches

Einloggen