Energieverteilung bei Teilchen

Gegenstand der kinetischen Gastheorie ist die Betrachtung thermodynamischer Prozesse auf der Grundlage von Teilchengrößen, wie der Teilchenanzahl, ihrer räumlichen Verteilung und ihrer Geschwindigkeit. Von besonderer Bedeutung ist die Energieverteilung, die eng mit der Geschwindigkeitsverteilung zusammenhängt. Betrachtet man verschiedene Aggregatzustände und bezieht auch Moleküle in die Betrachtungen ein, so ist neben der kinetischen Energie auch die Rotationsenergie und die Schwingungsenergie mit zu beachten.

Gegenstand der kinetischen Gastheorie ist die Betrachtung thermodynamischer Prozesse auf der Grundlage von Teilchengrößen, wie der Teilchenanzahl, ihrer räumlichen Verteilung und ihrer Geschwindigkeit. Von besonderer Bedeutung ist die Energieverteilung, die eng mit der Geschwindigkeitsverteilung zusammenhängt. Betrachtet man verschiedene Aggregatzustände und bezieht auch Moleküle in die Betrachtungen ein, so ist neben der kinetischen Energie auch die Rotationsenergie und die Schwingungsenergie mit zu beachten.

Bewegung von Atomen und Molekülen und ihre Energie
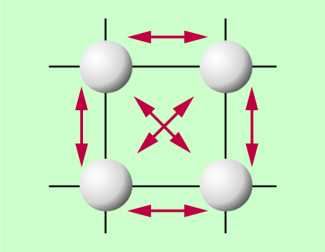
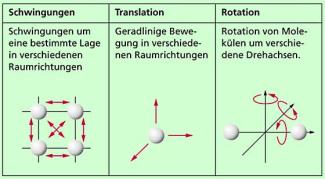
Atome und Moleküle eines Stoffes bewegen sich ständig ungeordnet. Die Geschwindigkeiten sind unterschiedlich, die Bewegungen können in verschiedener Weise erfolgen. Welche Bewegungen möglich sind, hängt vom Aggregatzustand und davon ab, ab Atome oder Moleküle vorliegen und wie sie aufgebaut sind. Einen Überblick über die wichtigsten Bewegungsmöglichkeiten und damit über mögliche Energien gibt Bild 2:

Bei festen Körpern können die Teilchen um eine Gleichgewichtslage schwingen. Sie haben damit kinetische Energie , deren Betrag von der Amplitude der Schwingungen abhängt.
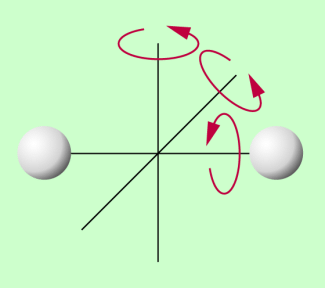
Bei Flüssigkeiten und Gasen können sich Atome bzw. Moleküle in den drei Raumrichtungen bewegen. Sie haben kinetische Energie. Bei zweiatomigen, hantelförmig angeordneten Molekülen kommt zu der möglichen translatorischen Bewegung noch eine Rotation um drei mögliche Achsen und damit die entsprechende Rotationsenergie hinzu. Dabei ist die Rotationsenergie um die Längsachse wegen des kleinen Trägheitsmoments um diese Achse so gering, dass sie meist vernachlässigt wird.

Energieverteilung beim idealen Gas
Beim idealen Gas haben die als Massepunkte angenommenen Teilchen nur kinetische Energie der Translation . Die Energieverteilung ergibt sich aus der Geschwindigkeitsverteilung der Teilchen. Genauere Informationen dazu sind unter dem Stichwort „ Geschwindigkeitsverteilung “ zu finden.
Beträgt die Geschwindigkeit eines Teilchens v, so ist die kinetische Energie:
$E_{kin} = \frac{1}{2} m \cdot v^{2}$
Die Geschwindigkeit der Teilchen schwankt aber in einem weiten Bereich. Für statistische Betrachtungen bedeutsamer ist die mittlere kinetische Energie der Teilchen, die sich ergibt, wenn man das mittlere Geschwindigkeitsquadrat ansetzt. Dann gilt für die mittlere kinetische Energie der Teilchen:
$\begin{array}{l} {\bar{E}}_{k i n} = \frac{1}{2} m \cdot \bar{v^{2}} \\ m Masse eines Teilchens \\ \bar{v^{2}} mittleres Geschwindigkeitsquadrat \end{array}$

Besteht ein Gas in einem Raumbereich aus N Teilchen, dann ist die gesamte Energie des Gases gleich der Summe der kinetischen Energien aller seiner Teilchen. Für das ideale Gas ist das zugleich die innere Energie U:

$\begin{array}{l} U = N \cdot {\bar{E}}_{kin} \\ N Teilchenanzahl \\ {\bar{E}}_{kin} mittlere kinetische Energie eines Teilchens \end{array}$

Verknüpft man die Grundgleichung der kinetischen Gastheorie in der Form
$p \cdot V = \frac{2}{3} N \cdot {\bar{E}}_{kin} (1)$
mit der Zustandsgleichung des idealen Gases in der Form
$p \cdot V = N \cdot k \cdot T (2)$

so erhält man durch Gleichsetzen der rechten Seiten der Gleichungen (1) und (2) den folgenden Zusammenhang:

$\begin{array}{l} {\bar{E}}_{k i n} = \frac{3}{2} k \cdot T \\ k BOLTZMANN-Konstante \\ T absolute Temperatur \end{array}$

Das bedeutet: Die mittlere kinetische Energie eines Teilchens hängt man der absoluten Temperatur ab. Das Teilchen kann sich, wie oben dargestellt, in drei Raumrichtungen bewegen. Auf jede der drei Raumrichtungen oder, wie man in der Physik auch sagt, auf jeden Freiheitsgrad entfällt dann im Mittel eine kinetische Energie von
${\bar{E}}_{kin} = \frac{1}{2} k \cdot T$

Ein einatomiges Gas hat drei Freiheitsgrade der Translation (3 Raumrichtungen), ein zweiatomiges Gas fünf Freiheitsgrade (Bild 3), nämlich drei Freiheitsgrade der Translation in den drei Raumrichtungen und drei Freiheitsgrade der Rotation (Bild 3), wobei aber der Freiheitsgrad um die Längsachse aufgrund des geringen Trägheitsmomentes und damit der geringen Rotationsenergie vernachlässigt wird. Im statistischen Mittel verteilt sich die Gesamtenenergie gleichmäßig auf die Freiheitsgrade. Damit erhält man zusammenfassend:

Energie für einen Freiheitsgrad	Energie für ein einatomiges Gas (3 Freiheitsgrade)	Energie für ein zweiatomiges Gas (5 Freiheitsgrade)
${\bar{E}}_{kin} = \frac{1}{2} k \cdot T$	${\bar{E}}_{kin} = \frac{3}{2} k \cdot T$	${\bar{E}}_{kin} = \frac{5}{2} k \cdot T$

Dabei bedeuten:

k
T

BOLTZMANN-Konstante
absolute Temperatur

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Energieverteilung bei Teilchen

Rechtliches

Einloggen