Grundgleichung der kinetischen Gastheorie

Herleitung der Grundgleichung der kinetischen Gastheorie

Der Ansatzpunkt für die Herleitung ist der Zusammenhang zwischen Teilchenbewegung und Gasdruck, wobei von den folgenden vereinfachenden Annahmen ausgegangen wird:

• Betrachtet wird ein ideales Gas, bei dem nur elastische Wechselwirkungen zwischen den Teilchen bzw. zwischen Teilchen und Gefäßwänden auftreten.
• Die Teilchen haben eine durchschnittliche Geschwindigkeit v.
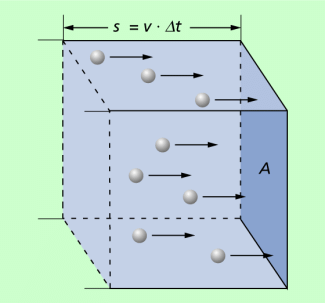
• Senkrecht zu jeder der sechs Flächen eines Würfels ( Bild 1) bewegen sich je 1/6 aller Teilchen. Das ist eine statistische Annahme, die an eine große Teilchenanzahl gebunden ist.
• Im Behälter mit dem Volumen V befinden sich insgesamt N Teilchen. Die Teilchenanzahldichte beträgt somit N/V. Sie kann statistisch als konstant im gesamten Raumgebiet angesehen werden.

In einem Quader der Seitenfläche A und der Länge $s=v\cdot \Delta t$(Bild 1) befindet sich dann eine Teilchenanzahl von:
$\begin{array}{l}\frac{N}{V}\cdot A\cdot v\cdot \Delta t\\ \end{array}$
Betrachten wir nur die Teilchen, die sich in Richtung Fläche A bewegen, dann sind das 1/6 der gesamten Teilchenanzahl, also:
$\frac{1}{6}\cdot \frac{N}{V}\cdot A\cdot v\cdot \Delta t$
Jedes einzelne Teilchen hat die Masse m und die Geschwindigkeit $\overrightarrow{v}$ und damit den Impuls $\overrightarrow{p}=m\cdot \overrightarrow{v}$
Nach einem geraden zentralen elastischen Stoß beträgt dieser Impuls , $-m\cdot \overrightarrow{v}$ hat also den gleichen Betrag, aber die entgegengesetzte Richtung. Der Betrag der Impulsänderung für ein Teilchen beträgt demzufolge bei der elastischen Wechselwirkung mit der Wand
$2m\cdot v.$
Betrachtet man alle Teilchen, die während des Zeitintervalls $\Delta t$ auf die Wand treffen, dann beträgt die Impulsänderung für alle diese Teilchen
$\begin{array}{l}\Delta p_i=\frac{1}{6}\cdot \frac{N}{V}\cdot A\cdot v\cdot \Delta t\cdot 2m\cdot v\text{(1)}\\ \text{Bezieht man den Zusammenhang zwischen Kraftstoß}\\ \text{und Impuls mit ein}\text{, dann gilt}F\cdot \Delta t=\Delta p_i\text{oder}\\ F=\frac{\Delta p_i}{\Delta t}\text{(2)}\\ \text{Setzt man Gleichung (1) in (2) ein}\text{, folgt:}\\ F=\frac{\frac{1}{6}\cdot \frac{N}{V}\cdot A\cdot v\cdot \Delta t\cdot 2m\cdot v}{\Delta t}\text{oder vereinfacht:}\\ F=\frac{1}{3}\cdot \frac{N}{V}\cdot A\cdot m\cdot v^2\\ \text{Die Division der Gleichung durch A ergibt:}\\ \frac{F}{A}=\frac{1}{3}\cdot \frac{N}{V}\cdot m\cdot v^2\\ \text{Der Quotient}F/A\text{ist der Druck}p,\text{sodass man auch}\\ \text{schreiben kann:}\\ p=\frac{1}{3}\cdot \frac{N}{V}\cdot m\cdot v^2\\ \text{Dafür kann man bei Multiplitation mit}\frac{\text{2}}{\text{2}}\text{auch schreiben:}\\ p=\frac{2}{3}\cdot \frac{N}{V}\cdot \frac{1}{2}m\cdot v^2\end{array}$
Der rechts stehende Term ist die kinetische Energie eines Teilchens unter der vereinfachenden Annahme, dass die mittlere Geschwindigkeit der Teilchen v beträgt. Beachtet man, dass als Mittelwert der Geschwindigkeit der Teilchen der quadratische Mittelwert der Geschwindigkeit angesetzt werden muss, dann erhält man aus der zuletzt genannten Gleichung:
$p=\frac{2}{3}\cdot \frac{N}{V}\cdot \frac{1}{2}m\cdot \overline{v^2}$

Diese Gleichung wird als Grundgleichung der kinetischen Gastheorie bezeichnet und häufig in folgender Form angegeben:
$\begin{array}{l}p\cdot V=\frac{1}{3}N\cdot m\cdot \overline{v^2}\\ p\text{Druck}\\ V\text{Volumen}\\ N\text{Teilchenanzahl}\\ m\text{Masse eines Teilchens}\\ \overline{v^2}\text{mittleres Geschwindigkeitsquadrat}\end{array}$