Interferenz an dünnen Schichten

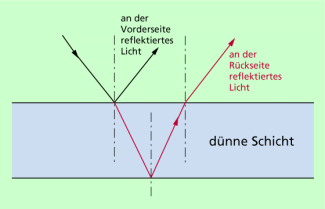
Die Flügel einer Libelle, eine dünne Ölschicht auf Wasser oder eine Seifenblase schillern in den unterschiedlichsten Farben. Ursache dafür ist die Interferenz von Licht, das auf eine dünne Schicht trifft und an der Vorder- und der Rückseite dieser Schicht reflektiert wird. Das an verschiedenen Stellen reflektierte Licht überlagert sich. Es kommt zu farbigen Interferenzmustern.
Wichtige Fälle, die sich auch gut mathematisch beschreiben lassen, sind die Interferenz an planparallelen Schichten und die Interferenz an keilförmigen Schichten. Ein spezieller Fall sind die newtonsche Ringe, mit deren Hilfe man z.B. die Qualität von Linsen prüfen kann.

Eigenschaften von Wellen

#Sinus #Cosinus #Frequenz #Wellenlänge #Periodendauer

Lichtstrahlen

#Schatten #Lichtstrahlen #Lichtquelle #Hell #dunkel #Halbschatten

(Bild 1) Wir betrachten nachfolgend unterschiedliche Fälle einer solchen Interferenz an dünnen Schichten.

Verlauf von Licht beim Auftreffen auf eine dünne Schicht

Trifft Licht auf eine dünne Schicht, so wird ein Teil des Lichtes an der Oberfläche reflektiert, ein Teil dringt in die dünne Schicht ein. Das eindringende Licht erreicht nach Durchqueren der Schicht dessen Rückseite, wird dort reflektiert und gelangt dadurch wieder in Richtung Vorderseite (Bild 2). Nach abermaligem Passieren der Grenzschicht eilt dieser Lichtanteil dem unmittelbar reflektierten hinterher. Da der ins Medium eindringende Lichtanteil einen längeren Weg bis zum Wiederaustritt durchläuft als der direkt reflektierte Teil, liegen nun im Allgemeinen nicht mehr gleiche Schwingungsphasen vor, sondern es ist ein Gangunterschied vorhanden.
Da sich dieser Gangunterschiede bei konstanter Mediendicke mit dem Einfallswinkel des Lichtes oder bei konstantem Einfallswinkel mit der Schichtdicke ändert, können im reflektierten und natürlich auch im durchfallenden Licht Interferenzen entstehen.
Die zur deren Untersuchung benutzten Verfahren lassen sich auch auf Netzgitterebenen von Kristallen übertragen und gestatten das Verständnis von Interferenzen an Kristallgitterebenen.
Bei der Reflexion an der Schicht und beim Durchgang des Lichtes durch die Schicht sind zwei Besonderheiten zu beachten:

Trifft Licht aus einem optisch dünneren Stoff kommend auf einen optisch dichteren Stoff, dann tritt bei der Reflexion ein Phasensprung von $λ / 2$ auf. Das wäre z.B. beim Übergang Luft-Glas oder Luft-Öl der Fall. Bei dem in Bild 2 beschriebenen Verlauf tritt stets ein Phasensprung von $λ / 2$ auf.
Beträgt die Wellenlänge von Licht im Vakuum und damit näherungsweise auch in Luft , $λ$ so hat sie in einem Stoff mit der Brechzahl n den Wert $λ / n$ . Das ergibt sich aus folgender Überlegung:

$\begin{array}{l} Mit \frac{c}{c_{Stoff}} = n und c = λ \cdot f \\ erhält man: \\ \frac{λ \cdot f}{λ_{Stoff} \cdot f} = n \\ Da sich die Frequenz beim Übergang von einem Medium \\ in ein anderes nicht ändert, kann man mit f kürzen und \\ erhält: \\ \frac{λ}{λ_{Stoff}} = n oder λ_{Stoff} = \frac{λ}{n} \end{array}$

Interferenz an planparallelen Schichten

Fällt das Licht senkrecht oder näherungsweise senkrecht auf eine planparallele Schicht , dann tritt bei der Reflexion Verstärkung (Maxima) auf, wenn:
$2 d = \frac{2 k + 1}{n} \cdot \frac{λ}{2} (k = 0, 1, 2,...)$
Entsprechend gilt für die Auslöschung bei der Reflexion von Licht (Minima):
$2 d = \frac{2 k}{n} \cdot \frac{λ}{2} (k = 1, 2, ...)$
Ob das reflektierte Licht verstärkt oder abgeschwächt wird, hängt also nur von der Schichtdicke und der Wellenlänge ab.
Im durchgehenden Licht gilt die erste Beziehung für die Minima, die zweite für die Maxima.

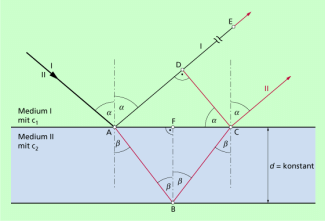
Etwas komplizierter sind die Zusammenhänge, wenn das Licht unter einem beliebigen anderen Winkel auf die dünne Schicht fällt (Bild 3). Wir betrachten dabei nur die nach dem ersten Reflexions- und Brechungsvorgang an der Vorderseite der dünnen Schicht vorhandenen Lichtbündel. In A, also beim Auftreffen auf die dünne Schicht, ist die Phase gleich. Während der eine Teil des Lichtes in A reflektiert wird, durchläuft der andere die dünne Schicht, wird an deren Rückseite reflektiert und tritt bei C wieder aus. Damit ist eine Phasendifferenz (ein Gangunterschied) zwischen dem in A reflektierten und dem in C austretenden Lichtbündel vorhanden. Wir nehmen dabei an, dass die Phase in C gleich der des anderen Lichtbündels in E ist. Von nun an verändert sich die Phasenlage nicht mehr.

Da die auf Bündel II in C liegende Phase neben der in Punkt D auf Bündel I liegt, hat die Phase auf I gegenüber der auf II den Vorsprung der Streckenlänge von D bis E.
Bei der Reflexion einer Welle am Ende eines Ausbreitungsmediums kann es zu einem Phasensprung kommen, sofern es sich um ein sogenanntes „festes Ende“ handelt. Für ein „loses Ende“ entsteht kein Phasensprung. Da die beiden Stellen A und B solche mit genau entgegengesetztem Brechungsverhalten sind, ist ein Übergang ein festes Ende, der andere ein loses Ende. Wichtig ist nur, daß es insgesamt einen Phasensprung von einer halben Wellenlänge gibt. Daraus ergibt sich für die beiden Lichtanteile ein Gangunterschied von $Δ s = \bar{DE} \pm \frac{λ}{2}$ .

Um die Strecke $\bar{DE}$ zu berechnen, beachtet man, dass die Strecke $\bar{AE}$ in der gleichen Zeit durchlaufen wird wie die Strecke . $\bar{AB} + \bar{BC} = 2 \cdot \bar{AB}$ Die Strecke $\bar{AC}$ wird von Einfallswinkel, $α$ vom Brechungswinkel $β$ und Schichtdicke d bestimmt. Damit sind alle Strecken über einfache trigonometrische Beziehungen darstellbar.
Dem Bild 3 entnimmt man:

\begin{array}{l} \bar{ED} = \bar{AE} - \bar{AD} \\ \bar{AE} = 2 c_{1} \cdot t_{\bar{AB}} \\ \bar{AD} = \bar{AC} \cdot \sin α \\ \bar{AC} = 2 d \cdot \tan β \end{array}

Aus den beiden letzten Gleichungen erhält man:

\bar{AD} = 2 d \cdot \tan β \cdot \sin α

Damit ist die Strecke zwischen A und D allein aus der Schichtdicke, dem Einfalls- und dem Brechungswinkel dargestellt.
Für die Strecke

\bar{AE}

verfährt man ähnlich:

\begin{array}{l} d : \bar{AB} = \cos β und damit: \\ \bar{AB} = \frac{d}{\cos β} \end{array}

Andererseits gilt: $\begin{array}{l} \bar{AB} = c_{2} \cdot t_{\bar{AB}} \\ t_{\bar{AB}} = \frac{d}{c_{2} \cdot \cos β} \end{array}$

Also ergibt sich für die Strecke zwischen A und E insgesamt:

\bar{AE} = \frac{2 c_{1} \cdot d}{c_{2} \cdot \cos β}

Nunmehr kann der Gangunterschied insgesamt allein aus der Schichtdicke des brechenden Mediums, dem Einfallswinkel sowie der Brechungszahl dargestellt werden.

$Δ s \pm \frac{λ}{2} = \frac{2 d \cdot \sin α}{\sin β \cdot \cos β} - \frac{2 d \cdot \sin β \cdot \sin α}{\cos β}$

Nach Ausklammern gemeinsamer Faktoren, Benutzung des Brechungsgesetzes und des trigonometrischen Pythagoras gewinnt man folgende Form:

$\begin{array}{l} Δ s \pm \frac{λ}{2} = \frac{2 d \cdot \sin α}{\cos β} (\frac{1}{\sin β} - \sin β) \\ Δ s \pm \frac{λ}{2} = \frac{2 d \cdot \sin α}{\cos β} (\frac{1 - \sin^{2} β}{\sin β}) \\ Δ s \pm \frac{λ}{2} = \frac{2 d \cdot \sin α}{\cos β} \cdot \frac{\cos^{2} β}{\sin β} \\ Δ s \pm \frac{λ}{2} = 2 d \cdot \cos β \cdot \frac{\sin α}{\sin β} \\ Δ s \pm \frac{λ}{2} = 2 d \cdot \cos β \cdot \frac{c_{1}}{c_{2}} \\ Δ s \pm \frac{λ}{2} = 2 d \cdot \frac{c_{1}}{c_{2}} \cdot \sqrt{1 - \sin^{2} β} \end{array}$

Da nach dem Brechungsgesetz $\sin β = \frac{c_{2}}{c_{1}} \cdot \sin α$ ist, erhält man:

$\begin{array}{l} Δ s \pm \frac{λ}{2} = \frac{2 d \cdot c_{1}}{c_{2}} \sqrt{1 - \frac{c_{2}^{2}}{c_{1}^{2}} \cdot \sin^{2} α} \\ Δ s \pm \frac{λ}{2} = 2 d \sqrt{\frac{c_{1}^{2}}{c_{2}^{2}} - \sin^{2} α} \\ Δ s \pm \frac{λ}{2} = 2 d \sqrt{n^{2} - \sin^{2} α} \end{array}$

Somit beträgt der Gangunterschied für das reflektierte Licht:

$Δ s = 2 d \sqrt{n^{2} - \sin^{2} α} \pm \frac{λ}{2}$

Für das durchfallende Licht treten dagegen zwei Reflexionen an gleichen Übergängen auf (nämlich an der inneren Rückseite der Schicht sowie an ihrer inneren Vorderseite). Das ergibt entweder den Phasensprung $λ$ bzw. 0. Deshalb ergibt sich für den Gangunterschied im durchgehenden Licht

$Δ s_{durchfallend} = 2 d \sqrt{n^{2} - \sin^{2} α}$

Aus beiden Gleichungen lassen sich Schlussfolgerungen ziehen sowie experimentell prüfbare Anordnungen entwickeln.

Betrachtung des reflektierten Lichtes
Die gefundene Beziehung zeigt, dass der Gangunterschied von vier Variablen bestimmt wird:

\begin{array}{l} Δ s = 2 d \sqrt{n^{2} - \sin^{2} α} \pm \frac{λ}{2}, d . h . für den Gangunterschied \\ gilt: \\ Δ s = f (d, n, α, λ) \end{array}

Bleibt man zunächst bei einem lichtdurchlässigen Medium, also n = konstant, so erkennt man, dass bei konstanter Schichtdicke (planparallele Schicht) für monochromatisches Licht für alle Lichtwege, die unter dem gleichen Einfallswinkel auf die Schicht treffen, der gleiche Gangunterschied entsteht.
Ordnet man also vor einer planparallelen Platte eine Quelle für monochromatisches Licht (z.B. eine Na-Dampflampe) so an, dass die Lichtwege, die diese Schicht unter dem gleichen Winkel treffen, mit der Schicht einen geraden Kegel bilden, so ergibt sich als Interferenzbild ein System konzentrischer Ringe. Benutzt man als planparallele Schicht eine Glimmer-Platte, erhält man eindrucksvolle Interferenzen, die eine Fläche von mehreren Quadratmetern bedecken können (pohlscher Versuch).
Würde man dagegen eine Lichtquelle verwenden (z.B. eine Hg-Dampflampe), die mehrere Farben emittiert, würde jede Farbe einen eigenen Ring liefern.
Derartige Interferenzen an Schichten konstanter Stärke heißen Kurven gleicher Neigung, da der Gangunterschied durch den Einfallswinkel bestimmt wird.

Betrachtung im durchgehenden Licht

Um Licht mit einem schmalen Wellenlängenbereich (im Idealfall monochromatisches Licht) zu erzeugen bietet sich die Möglichkeit des Einsatzes geeigneter Filter an. Allein farbige Gläser sind nur eine unbefriedigende Lösung, da sie einen breiten Wellenlängenbereich passieren lassen.
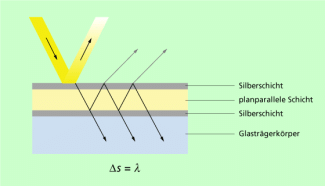
Einen Ausweg bieten sogenannte Metallinterferenz-Filter (Bild 4). Auf einen Glaskörper wird eine sehr dünne Silberschicht aufgedampft. Der Herstellungsvorgang sichert, dass diese extrem plan ist. Darauf wird eine Parallelschicht aus lichtdurchlässigem Material aufgedampft, auf die abermals eine Silberschicht folgt. Die Schichtdicke der eingeschlossenen Schicht so wird gewählt, daß im durchfallenden Licht für genau eine geforderte Wellenlänge maximale Verstärkung auftritt.
Das auf die vordere Silberschicht auftreffende Licht (a) wird zu einem großen Teil direkt reflektiert (b). Das eindringende Licht (Metalle der Dicke weniger Mikrometer lassen Licht hindurch) erreicht nach Durchlaufen der planparallelen Schicht die untere Silberschicht. Ein Teil geht hindurch, ein Teil wird wiederum zur vorderen Schicht reflektiert und erneut in einen austretenden und einen wieder zur unteren Silberschicht reflektierten Anteil gespalten, von dem ebenfalls der eben geschilderte Vorgang wiederholt wird.
Dadurch entstehen wegen der häufigen Reflexionen viele Teilbündel, die durch die hintere Silberschicht austreten. Sie haben aufgrund der gleichen Wege alle den gleichen Gangunterschied, der von der Dicke der Planschicht bestimmt ist. Dadurch ist das durchfallende Licht praktisch einfarbig (monochromatisch). Unterstützt wird der Vorgang noch dadurch, dass die Glasträgerschicht durch ihre Einfärbung den Effekt unterstützt.
Derartige Metallinterferenz-Filter scheinen bei Betrachtung von der versilberten Seite wie ein hochwertiger Spiegel. Erst wenn man sie dem Auge stark annähert, erkennt man, dass man hindurch blicken kann.
Eine etwas billigere Variante kann man für Lichtquellen bauen, die nur wenige Wellenlängen in ihrem Spektrum haben (z.B. Hg-Dampf-Lampe), da hierzu eine aufgedampfte Metallschicht ausreicht.

Mit einem Aufdampfverfahren wird auch für hochwertige optische Linsen die Reflexionsfähigkeit herabgesetzt. Ein großer Spektralbereich wird dadurch im reflektierten Licht ausgelöscht. Deshalb erscheinen diese vergüteten Linsen im reflektierten Licht bläulich. Das in der Reflexion fehlende Licht ist natürlich im durchfallenden Licht enthalten.

Interferenz an keilförmigen Schichten

Ausgangspunkt der Betrachtungen ist wiederum die oben abgeleitete Gleichung für den Gangunterschied zwischen Licht, das an der Vorder- und Rückseite einer dünnen Schicht reflektiert wird:
$Δ s = 2 d \sqrt{n^{2} - \sin^{2} α} \pm \frac{λ}{2}$
Lässt man neben der Brechzahl n auch den Einfallswinkel konstant, so entstehen Interferenzen auch durch Veränderung der Schichtdicke d. Wählt man zur Vereinfachung senkrechten Lichteinfall, so reduziert sich die Gleichung für den Gangunterschied zu:

Δ s = 2 d \cdot n \pm \frac{λ}{2}

Da für einfarbiges Licht der Gangunterschied allein von der Dicke der lichtdurchlässigen Schicht bestimmt wird, entsteht für einen festen Wert von $Δ s$ an allen Stellen, die eine gleiche Schichtstärke haben, das gleiche Interferenzergebnis. Derartige Interferenzen nennt man Kurven gleicher Dicke.

Betrachtet man etwa die Stellen maximaler Verstärkung, so gilt dafür die Bedingung:
$Δ s = 2 k \cdot \frac{λ}{2}$
Daraus kann man die Schichtstärken für maximale Verstärkung im reflektierten Licht ermitteln:
$2 k \cdot \frac{λ}{2} = 2 d \cdot n \pm \frac{λ}{2}$
Hieraus folgt:
$d_{Verstärkung} = (2 k \pm 1) \frac{λ}{4 n}$

Analog erhält man für Zonen vollständiger Auslöschung wegen
die Schichtstärken:
$d_{Auslöschung} = 2 k \frac{λ}{4 n}$

Aufeinanderfolgende Zonen maximaler Verstärkung (ebenso wie die der vollständigen Auslöschung) haben stets den Schichtdickenunterschied
$Δ d = 2 \frac{λ}{4 n}$ , sofern die Wellenlänge konstant bleibt.

Gerade Interferenzstreifen und newtonsche Ringe

Einen solchen linearen Schichtdickenzuwachs kann man durch einen Luftspalt zwischen zwei ebenen Glasflächen erzeugen, die man aufeinanderlegt und zwischen die man an einer Seite einen dünnen Gegenstand (etwa eine Rasierklinge) bringt. Von der direkten Auflagekante in Richtung auf den eingefügten Gegenstand vergrößert sich die Schichtdicke linear, sofern die einander zugewandten Flächen völlig plan sind.
Für Na-Licht mit einer Wellenlänge von 589 nm erhält man für die ersten Streifen maximaler Verstärkung (1., 2. und 3.Ordnung) die Schichtdicken 221 nm, 662 nm und 1.103 nm, dagegen für die der vollständigen Auslöschung 0 nm, 442 nm und 884 nm.
Im Falle völlig ebener Glasflächen ergeben sich so parallele helle und dunkle gerade Interferenzstreifen. Jede Abweichung von der Geradlinigkeit deutet auf eine Unebenheit der Glasflächen hin. Damit verfügt man über ein sehr genaues Prüfverfahren, um die Formgleichheit eines Prüflings aus lichtdurchlässigem Material mit einem mit äußerster Präzision gefertigten Normal festzustellen: Sind beide völlig identisch, muss im reflektierten Licht die gesamte Auflagefläche dunkel bleiben. Jede Aufhellung stellt eine Abweichung von der angestrebten Form dar.

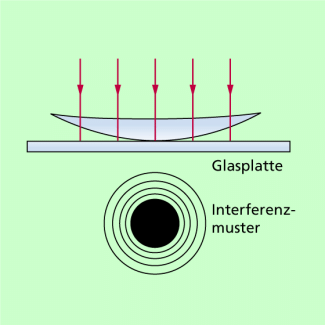
Besonders deutlich werden solche Interferenzen, wenn auf eine Konkavlinse eine Konvexlinse fast identischer Form gelegt wird. An einer derartigen Anordnung hat ISAAC NEWTON (1643-1727) diese Kurven gleicher Dicke erstmals beobachtet und auch eine Erklärung für ihr Zustandekommen gegeben. Allerdings musste er dazu eine gewisse Periodizität der von ihm zur Lichtbeschreibung benutzten Korpuskeln als Kompromiss zulassen. Da bei exaktem Schliff beider Glaskörper die Zonen mit gleicher Schichtstärke konzentrische Kreise um die Auflagestelle sind, zeigen sich die Interferenzkurven gleicher Ordnung als Ringe, weshalb man sie als newtonsche Ringe (Bild 5) bezeichnet.
Für Demonstrationsversuche gibt es eine Anordnung, bei der die beiden Linsenkörper durch zwei Spannringe zusammengehalten werden. Durch Spannschrauben lässt sich der Andruck der beiden Glaskörper verändern. Das führt sofort zu einer Formänderung der newtonschen Ringe.
Wenn beide Keil bildenden Stoffe lichtdurchlässig sind, kann man die Interferenzfiguren auch im durchfallenden Licht beobachten.
Nimmt man z.B. an, dass die den Keil begrenzenden Schichten aus dem gleichen Material bestehen (also etwa beide aus Glas), so beträgt der Gangunterschied wegen des zweimaligen Auftretens des Phasensprungs an den Grenzschichten $Δ s = 2 d \cdot n$ .
Er unterscheidet sich von dem für das reflektierte Licht für den gleichen Gangunterschied also stets um eine halbe Wellenlänge. Das bedeutet, dass im durchfallenden und reflektierten Licht an der gleichen Stelle der Schicht komplementäre Interferenzergebnisse entstehen. Während also bei den newtonschen Ringen im reflektierten Licht die Auflagestelle der beiden Glaskörper dunkel ist ( $Δ s = \frac{λ}{2}$ , denn d = 0), ist sie im durchfallenden Licht ein Gebiet für maximale Verstärkung da der Gangunterschied dann null ist.

Schillernde Seifenblasen und bunte Ölschichten

Zu den auffallendsten Erscheinungen, an denen Interferenzen an dünnen keilförmigen Schichten beteiligt sind, gehören z.B. Seifenblasen , die in allen Spektralfarben leuchten, ebenso wie farbig schimmernde Ölschicht auf einer Wasserfläche. In beiden Fällen handelt es sich um den gleichen Vorgang: Unter dem Einfluss der Schwerkraft verteilt sich ein Ölfilm auf einer Trägerschicht (meist Wasser) zu einer keilförmigen Schicht. Da die Beobachtung meist bei natürlicher Beleuchtung stattfindet, werden die Spektralfarben an verschiedenen Schichtstärken (wegen ihrer verschiedenen Wellenlängen) maximal verstärkt, weshalb derartige Objekte in den Regenbogenfarben leuchten.

Erzeugt man mit einer Seifenlösung durch Eintauchen eines Drahtbügels bei dessen Herausziehen eine Seifenhaut, so kann man beobachten, dass sich die Farbbereiche nach unten verschieben und die Seifenfläche unmittelbar vor dem Zerplatzen an der Oberseite im reflektierten Licht fast schwarz wird.
Durch das Verlaufen der Lösung wird die Schicht an der Oberkante immer dünner, sodass sie endlich zerreißt.

Lernprobleme in Physik?

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

KI-Tutor Kim hilft bei allen schulischen Problemen
Individuelle, kindgerechte Förderung in Dialogform
Lernplattform für 9 Fächer ab der 4. Klasse
Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
Rund um die Uhr für dich da

Jetzt in Physik durchstarten

Verwandte Artikel

Angaben zum Lexikon

Impressum