Isochore Zustandsänderungen

Bei einer isochoren Zustandsänderung eines Gases bleibt das Volumen konstant. Die Zustandskurve im p-V-Diagramm verläuft vertikal, parallel zur p-Achse. Ein solcher Prozess wird realisiert, wenn Gas in einem geschlossenen Behälter erwärmt wird. Die zugeführte Wärme führt zu einer Erhöhung der Temperatur und damit zu einer Änderung der inneren Energie U. Da das Volumen konstant bleibt, wird von dem Gas keine Arbeit verrichtet. Nach dem 1. Hauptsatz der Thermodynamik ist damit die zugeführte Wärme gleich der Änderung der inneren Energie des Gases:

$Q = Δ U$

Bei Verwendung des Modells ideales Gas erhöht die zugeführte Wärme die inneren Energie des Gases bei einem isochoren Prozess um:

$\begin{array}{l} Δ U = \frac{3}{2} N \cdot k \cdot Δ T \\ N Anzahl der Teilchen \\ k BOLTZMANN-Konstante \\ Δ T Temperaturdifferenz \end{array}$

Daraus lässt sich die molare Wärmekapazität eines idealen Gases bei konstantem Volumen berechnen.

Wärmezufuhr

#Wärme #innere Energie #Temperatur #Thermometer #Kelvin #Grad-Celsius

Die allgemeine Zustandsgleichung für Gase gibt die Beziehungen zwischen den thermischen Zustandsgrößen Druck, Temperatur und Volumen an. In vielen Fällen kann bei der Untersuchung thermodynamischer Prozesse zur Vereinfachung eine oder auch mehrere Zustandsgrößen als konstant angenommen werden.

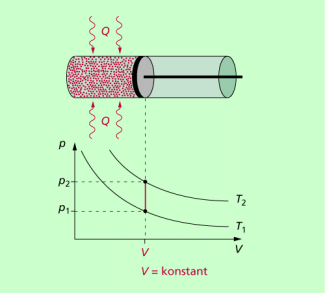
Bei einer isochoren Zustandsänderung bleibt das Volumen des Gases konstant. Die Zustandskurve im p-V-Diagramm verläuft vertikal, parallel zur p-Achse (Bild 1). Man bezeichnet sie auch als Isochore. Eine isochore Zustandsänderung erfolgt, wenn einem eingeschlossenem Gas von außen eine Wärme Q zugeführt wird. Die zugeführte Wärme Q erhöht die Temperatur des eingeschlossenen Gases und damit seine innere Energie. Mit dem Ansteigen der Temperatur erhöht sich die kinetische Energie der Gasteilchen, was zu einem Druckanstieg führt. Da das Volumen konstant bleibt, wird die gesamte zugeführte Wärme Q in innere Energie des Gases umgewandelt. Das Gas verrichtet keine Volumenarbeit.

Material zum Thema

BWS-PHY2-0177-03.htm

BWS-PHY2-0177-03.htm

Quantitative Zusammenhänge

Bei einer isochoren Zustandsänderung gilt mit V = konstant für den Zusammenhang zwischen Druck p und Temperatur T die Beziehung:
$\frac{p}{T} = konstant oder \frac{p_{1}}{T_{1}} = \frac{p_{2}}{T_{2}}$
Nach dem 1. Hauptsatz der Thermodynamik ergibt sich die folgende Bilanz:

$Q = Δ U$

Bei Verwendung des Modells ideales Gas kann die Änderung der inneren Energie des Gases bei einer isochoren Zustandsänderung berechnet werden. Die innere Energie des Gases im Ausgangszustand ist:

$\begin{array}{l} U = N \cdot {\bar{E}}_{k i n} = \frac{3}{2} N \cdot k \cdot T \\ N Anzahl der Teilchen \\ {\bar{E}}_{k i n} mittlere kinetische Energie \\ der Teilchen \\ k BOLTZMANN-Konstante \\ T absolute Temperatur \end{array}$

Nach Zuführung der Wärme Q erhöht sich die Temperatur des Gases um $Δ T$ und die innere Energie um $Δ U$ . Die innere Energie im Endzustand nach Aufnahme der Wärme Q ist daher:
$U + Δ U = \frac{3}{2} N \cdot k \cdot (T + Δ T)$
Die Änderung der inneren Energie ergibt sich daraus zu:
$Δ U = \frac{3}{2} N \cdot k \cdot Δ T$
Die Teilchenzahlzahl N kann durch die Stoffmenge n und die universelle Gaskonstante R ersetzt werden. Aus
$N = n \cdot N_{A} u n d R = N_{A} \cdot k$
ergibt sich für die Änderung der inneren Energie:
$\begin{array}{l} Δ U = \frac{3}{2} n \cdot N_{A} \cdot k \cdot Δ T = \frac{3}{2} n \cdot R \cdot Δ T \\ Δ U = n \cdot C_{mV} \cdot Δ T \end{array}$
Die konstante Größe
$C_{mV} = \frac{5}{2} R = 20,8 \frac{kJ}{K \cdot kmol}$
ist die molare Wärmekapazität bei konstantem Volumen. Sie ist für alle einatomigen Gase annähernd gleich groß.

Für zweiatomige Gase müssen bei der Berechnung der molaren Wärmekapazität neben den Freiheitsgrade n der Translation auch zwei Freiheitsgrade der Rotation berücksichtigt werden, da sich die kinetische Energie der Teilchen gleichmäßig auf alle Freiheitsgrade verteilt (Gleichverteilungssatz). Damit gilt für diesen Fall:

$C_{mV} = \frac{5}{2} R = 20,8 \frac{kJ}{K \cdot kmol}$

Aus der molaren Wärmekapazität können auch theoretische Werte der spezifischen Wärmekapazitäten $c_{V}$ bei konstantem Volumen einzelner Gase leicht bestimmt werden. Für das einatomige Edelgas Argon ergibt sich z.B.:

$c_{V} = \frac{C_{mV}}{M} = \frac{12,5 kJ \cdot kmol}{39,95 kg \cdot K \cdot kmol} = 0,31 \frac{kJ}{K \cdot kg}$

Für das zweiatomige Gas Sauerstoff folgt:

$c_{V} = \frac{C_{mV}}{M} = \frac{20,8 kJ \cdot kmol}{31,99 kg \cdot K \cdot kmol} = 0,65 \frac{kJ}{K \cdot kg}$

Diese theoretisch berechneten Werte stimmen mit den experimentell ermittelten Werten gut überein.
Mit der Einführung der spezifischen Wärmekapazität bei konstantem Volumen und Ersetzen der molaren Masse M durch die Masse m des Gases

$C_{mV} = c_{V} \cdot M und m = n \cdot M$

ergibt sich für die Änderung der inneren Energie bei einer isochoren Zustandsänderung:

$Δ U = n \cdot C_{mV} \cdot Δ T = m \cdot c_{V} \cdot Δ T$

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Isochore Zustandsänderungen

Wärmezufuhr

BWS-PHY2-0177-03.htm

Quantitative Zusammenhänge

Rechtliches

Einloggen