Kapillarität
Dass sich ein Stück Würfelzucker mit Tee vollsaugt, auch wenn man nur ein kleines Stück des Zuckers in den Tee hält, ist eine Folge der Kapillarität. Auch die Saugwirkung von bestimmten Tüchern oder das Aufsteigen von Wasser im Boden wird durch die Kapillarität bewirkt
Feuchte Wände bei einem Haus kommen zustande, wenn die Grundmauern, die sich im feuchten Erdreich befinden, nicht ausreichend isoliert sind. Dann kann Wasser durch die Poren in den Ziegelsteinen allmählich nach oben steigen und zu feuchten Wänden führen. Hier hilft nur eine Isolierung der Grundmauern mit wasserundurchlässigen Schichten.
Bringt man angefärbtes Wasser in ein Gefäß mit verbundenen Röhren, die eine sehr unterschiedliche Querschnittsfläche haben, dann zeigt sich: Je kleiner der Radius der Röhre ist, desto höher steigt das Wasser.
Kapillarität - Versuchsdurchführung
Vogt, Patrik, Landau
Herleitung der kapillaren Steighöhe h
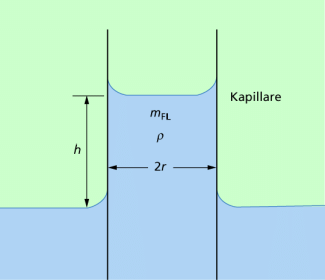
Das in Bild 1 dargestellte Experiment zeigt, dass die kapillare Steighöhe h in einer Kapillare von deren Radius r abhängig ist. Wie sie berechnet werden kann, soll nun hergeleitet werden.
Das oberhalb des Wasserspiegels stehende Wasser im Röhrchen (Bild 2) hat die Gewichtskraft:
Die Masse der überstehenden Flüssigkeit kann man ersetzen durch das Produkt aus deren Volumen und deren Dichte. Es gilt dann:
Das Volumen des betrachteten Kapillarenstücks kann wie das eines Zylinders berechnet werden. Durch Einsetzen folgt:
Dabei ist h die gesuchte Steighöhe. Die Flüssigkeitssäule befindet sich in Ruhe, d.h. es ist ein Kräftegleichgewicht vorhanden. Die Kraft, die der Gewichtskraft entgegenwirkt, ist die von der Oberflächenspannung herrührende Kraft F. Für diese Kraft gilt:
Nun können wir die beiden Kräfte gleichsetzen:
Kürzen und Auflösen nach der Steighöhe h führt zu der gesuchten Beziehung
Für einen bestimmten Stoff hängt die Steighöhe also nur von dem Radius des Röhrchens ab.
Zu beachten ist, dass diese Beziehung nur für den Fall einer vollkommen benetzenden Flüssigkeit gilt. Eine benetzende Flüssigkeit steht in einem Gefäß am Rand höher als in der Mitte. Sie bildet auf einer ebenen Fläche einen linsenförmigen Tropfen. Das gilt z.B. für Wasser.
Eine nicht benetzende Flüssigkeit steht dagegen in einem Gefäß am Rand niedriger als in der Mitte. Sie bildet auf einer ebenen Fläche kleine Kügelchen. Eine solche nicht benetzende Flüssigkeit ist z.B. Quecksilber. Bei solchen nicht benetzenden Flüssigkeiten tritt folgender Effekt auf: In einer Kapillare steigt die Flüssigkeit nicht nach oben, sondern sinkt nach unten. Das kann man am Beispiel von Quecksilber leicht zeigen.
Beispiel für Wasser
Die kapillare Steighöhe von Wasser soll für ein Röhrchen mit einem Radius von 1 mm berechnet werden. Die Dichte von Wasser beträgt und die Oberflächenspannung .
Unter den gegebenen Bedingungen würde das Wasser etwa 14 mm hoch stehen.
Die Steighöhe hängt bei einem bestimmten Stoff nur vom Radius des Röhrchens ab.
Ein Angebot von 