Kraftumformende Einrichtungen im Überblick
Alle einfachen mechanischen Anlagen, mit deren Hilfe man den Betrag oder die Richtung von Kräften oder beides verändern kann, werden als kraftumformende Einrichtungen bezeichnet. Zu diesen kraftumformenden Einrichtungen gehören die verschiedenen Arten von Hebeln, feste und lose Rollen, Flaschenzüge und geneigte Ebenen. Auch hydraulische und pneumatische Anlagen kann man zu ihnen zählen.
Für alle kraftumformenden Einrichtungen gilt die Goldene Regel der Mechanik.
Genauere Informationen zu den einzelnen kraftumformenden Einrichtungen sind unter den betreffenden Stichwörtern zu finden.
-
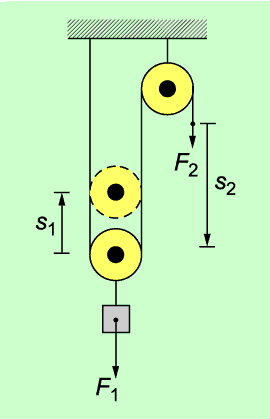
Rollen sind kraftumformende Einrichtungen
Walther-Maria Scheid, Berlin
Allgemeine Zusammenhänge
Einige Aussagen gelten für beliebige kraftumformende Einrichtungen, also für einen zweiseitigen Hebel ebenso wie für eine geneigte Ebene, einen Flaschenzug oder eine hydraulische Anlage. Mit kraftumformenden Einrichtungen ist es zwar möglich, Betrag oder Richtung der aufzuwendenden Kraft oder beides zu ändern. Es kann mit ihnen aber keine mechanische Arbeit gespart werden. Da bei allen technischen Anordnungen Reibung auftritt, ist in der Praxis die aufzuwendende Arbeit sogar immer größer als die nutzbringende Arbeit.
Unter der Bedingungen, dass die Reibung vernachlässigt werden kann, gilt für alle kraftumformenden Einrichtungen die Goldene Regel der Mechanik:
Dieses Gesetz wird wurde von dem italienischen Naturforscher GALILEO GALILEI (1564-1642) wie folgt formuliert:
Was man an Kraft spart, muss man an Weg zusetzen.
Man kann auch formulieren, dass aufzuwendende Arbeit und nutzbringende Arbeit unter der Bedingung, dass die Reibung vernachlässigt wird, gleich groß sind. In diesem Zusammenhang spricht man vom Gesetz von der Gleichheit der mechanischen Arbeit. Dabei sind folgende einschränkenden Bedingungen stets zu beachten: Die angegebenen Zusammenhänge gelten nur bei Vernachlässigung der Reibung. Bei Rollen und Flaschenzügen sind darüber hinaus die Gewichtskräfte der Rollen und Seile zu berücksichtigen.
Daraus folgt:
- Die Goldene Regel der Mechanik gilt in der Praxis nur näherungsweise. Ob die genannten Gleichungen angewendet werden dürfen, muss jeweils geprüft und abgeschätzt werden.
- Bei einer realen technischen Anordnung ist die aufzuwendende Arbeit immer größer als die nutzbringende Arbeit.
-
Die aufzuwendende Arbeit ist mindestens gleich der nutzbringenden Arbeit.