Leitung in Metallen
Leitungsvorgänge in Metallen
Metallische Leiter werden in vielfältiger Weise genutzt: als Kabel und Stromleitungen, als Glühwendel einer Glühlampe, als Verbindungsleiter, als Blitzableiter oder als Drahtwiderstand.
Damit in einem metallischen Leiter ein Strom fließt und damit ein elektrischer Leitungsvorgang vor sich geht, müssen wie bei beliebigen anderen Leitungsvorgängen auch zwei Voraussetzungen erfüllt sein:
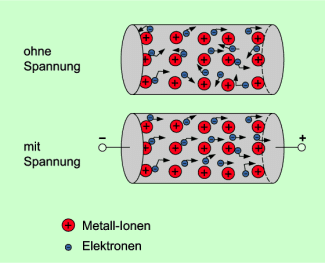
- Es müssen frei bewegliche (wanderungsfähige) Ladungsträger vorhanden sein: Bei Metallen existieren aufgrund der Metallbindung Elektronen, die sich im Metall nahezu frei bewegen können. Man spricht auch von einem Elektronengas (Bild 1).
- Es muss im betreffenden Raumbereich ein elektrisches Feld existieren: Das wird durch Anlegen einer elektrischen Spannung zwischen den Ende des metallischen Leiters erreicht.
Der Verlauf des elektrischen Leitungsvorganges in Metallen ist dann dadurch gekennzeichnet, dass
- sich Elektronen im Metall in einer Vorzugsrichtung gerichtet bewegen; die Geschwindigkeit in dieser Vorzugsrichtung wird als Driftgeschwindigkeit bezeichnet
- die gerichtete Bewegung der Elektronen durch Zusammenstöße mit den Metall-Ionen, die Schwingungen um eine Gleichgewichtslage ausführen, behindert wird. Je höher die Temperatur des Metalls ist, desto intensivere Schwingungen führen die Ionen aus, desto mehr werden die Elektronen behindert. Äußerlich bemerkt man diesen Sachverhalt anhand der Temperaturabhängigkeit des ohmschen Widerstandes der Metalle. Dabei wird elektrische Energie in thermische Energie umgewandelt. Diese thermische Energie wird in Form von Wärme oder Licht an die Umgebung abgegeben.
Metallbindung - Ursache für das Elektronengas
Die Metallbindung ist eine Art der chemischen Bindung, die durch Anziehungskräfte zwischen Metall-Ionen und freien Elektronen verursacht wird. Die meisten Metalle der Hauptgruppen besitzen nur wenige Außenelektronen, oft 1 bis 3. Diese Außenelektronen der Metalle können leicht vom Metall-Atom abgegeben werden, da die Atomkerne auf die Außenelektronen nur geringfügige Anziehungskräfte ausüben. Dadurch entstehen positiv geladene Metall-Ionen und nahezu frei bewegliche Elektronen. Diese frei beweglichen Elektronen ermöglichen die gute elektrische Leitfähigkeit und die hohe Wärmeleitfähigkeit der Metalle.
Man bezeichnet die freien Elektronen im metallischen Festkörper auch als Elektronengas - häufig nennt man sie nach dem italienischen Physiker ENRICO FERMI (1901-1954) auch Fermigas. Die hohe Beweglichkeit der Elektronen des Fermigases führt dazu, dass beim Anlegen eines elektrischen Feldes eine gerichtete Bewegung der Elektronen erfolgt. Allerdings darf man sich die Elektronenbewegung im Metall nicht als völlig geordnet vorstellen. Ähnlich wie die Teilchen eines idealen Gases bewegen sich auch die Elektronen in verschiedenen Raumrichtungen. Ein elektrisches Feld verleiht ihnen zusätzlich zu dieser ungeordneten Bewegung eine gerichtete Geschwindigkeitskomponente, sodass die Ladungsträger in einer bestimmten Richtung zu driften beginnen. Daher rührt die Bezeichnung Driftgeschwindigkeit für diese Geschwindigkeitskomponente. Sie liegt bei den üblichen Stromstärken bei metallischen Leitern in der Größenordnung von Millimetern je Sekunde.
Dichte und Beweglichkeit von Ladungsträgern
Die Ladungsträgerdichte n, auch Ladungsträgerkonzentration genannt, ist gleich der Anzahl der Ladungsträger in der Volumeneinheit. Sie wird folgendermaßen definiert:
Damit gilt für Elektronen im metallischen Leiter auch:
Dieser Ausdruck wird auch als räumliche Ladungsdichte bezeichnet. Bei guten Leitern kann man davon ausgehend, dass auf jedes Atom ein frei bewegliches Elektron kommt.
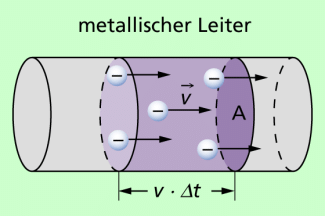
Über die Stromstärke im Leiter kann eine Gleichung zur Berechnung der Driftgeschwindigkeit hergeleitet werden. Wir betrachten dazu einen Leiter, wie er in Bild 2 dargestellt ist.
Dann gilt für die Stromstärke im Leiter:
Der Quotient U/l ist die elektrische Feldstärke E im Leiter. Damit ergibt sich als Gleichung für die Driftgeschwindigkeit:
Die Ladungsträgerbeweglichkeit u ist folgendermaßen definiert:
Ersetzt man in der oben genannten Gleichung
Das ist das Widerstandsgesetz für metallische Leiter, das man auch experimentell ableiten kann.
Ladungsträgerdichte, Beweglichkeit der Ladungsträger und elektrischer Widerstand
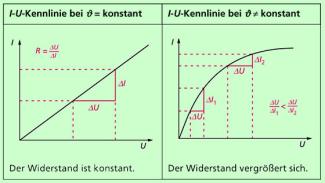
Bei konstanter Temperatur sind bei metallischen Leitern Ladungsträgerdichte und Beweglichkeit der Ladungsträger konstant. Damit ist auch der elektrische Widerstand konstant (Bild 3). Mit Erhöhung der Temperatur bleibt die Ladungsträgerdichte konstant, die Beweglichkeit verringert sich aber aufgrund der heftigeren Bewegungen der Metall-Ionen. Damit vergrößert sich mit Temperaturerhöhung der elektrische Widerstand (Bild 3).
Die elektrische Leitfähigkeit metallischer Leiter kann auch mithilfe des Bändermodells erklärt werden. Unter diesem Stichwort „Bändermodell“ ist ein gesonderter Beitrag auf der CD enthalten.
Energieumwandlungen in metallischen Leitern
Bei Stromfluss in einem metallischen Leiter wird ein Teil der elektrischen Energie in thermische Energie umgewandelt. Man spricht auch von der Stromwärme oder der jouleschen Wärme, weil die Energie in der Regel in Form von Wärme an die Umgebung abgegeben wird. Für diese Energie gilt:
Eine Verdopplung der Stromstärke im Leiter bedeutet damit eine Vervierfachung der thermischen Verluste, die man auch als Leitungsverluste bezeichnet.
Eine interessante Anwendung:Metall-Widerstandsthermometer
In einem Metall-Widerstandsthermometer nutzt man die Abhängigkeit des ohmschen Widerstandes von der Temperatur. Mit der Veränderung dieses Widerstandes geht eine Erhöhung oder Verringerung der fließenden Stromstärke bzw. der am Bauelement anliegenden Spannung einher. Beide Größen können gemessen werden und dienen nach entsprechender Eichung zur Angabe von entsprechenden Temperaturwerten. Einfache ohmsche Widerstände zeigen eine lineare Temperaturabhängigkeit. Das bedeutet, dass die Temperatur über weite Bereiche hinweg näherungsweise direkt proportional zum Widerstand, bei einer konstanten Spannung demzufolge indirekt proportional zur Stromstärke ist. Dieser Umstand ist von Vorteil, wenn man die gemessenen Stromstärken als Temperaturwerte eichen will. Nachteilig wirkt sich beim Einsatz normaler Widerstände aus, dass ihre Veränderung innerhalb kleiner Temperaturschwankungen ebenfalls nur sehr klein ist. Entsprechend empfindlich muss die Messanordnung sein. Häufig bedient man sich deshalb einer Brückenschaltung, bei der neben dem Messwiderstand noch drei weitere Vergleichswiderstände herangezogen werden.
elektrische Leitung in Metallen Driftgeschwindigkeit Berechnung Ladungsträgerkonzentration Wärmeleitfähigkeit elektrische Leitungsvorgänge räumliche Ladungsdichte Ladungsträgerbeweglichkeit Metall-Widerstandsthermometer elektrischer Widerstand Beweglichkeit der Ladungsträger elektrische Leitfähigkeit joulesche Wärme Leitungsverluste Fermigas Ladungsträgerdichte Brückenschaltung metallische Leiter Widerstandsgesetz frei bewegliche Elektronen wanderungsfähige Elektronen Metall-Ionen Metallbindung Stromwärme Simulation Rechenbeispiel Bändermodell Elektronengas
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 