- Lexikon
- Physik Abitur
- 1 Die Physik - eine Naturwissenschaft
- 1.2 Denk- und Arbeitsweisen in der Physik
- 1.2.5 Lösen physikalisch-mathematischer Aufgaben
- Lösen physikalischer Aufgaben mithilfe grafischer Mittel
Lösen physikalischer Aufgaben mithilfe grafischer Mittel
Dabei sollte man in folgenden Lösungsschritten vorgehen:
- Stelle physikalische Zusammenhänge zwischen Größen in einem Diagramm dar!
- Lies aus dem Diagramm wichtige Wertepaare ab!
- Interpretieren diese Werte bzw. den Kurvenverlauf!
Beispiel 1:
Ein Radfahrer fährt mit einer Geschwindigkeit von 18 km/h eine Straße entlang, ein Pkw in der gleichen Richtung mit 36 km/h. Zu einem bestimmten Zeitpunkt t befindet sich der Pkw 100 m hinter dem Radfahrer.
a) Nach welcher Zeit hat der Pkw den Radfahrer eingeholt?
b) Welche Wege haben in dieser Zeit Pkw und Radfahrer zurückgelegt?
Analyse:
Pkw und Radfahrer werden vereinfacht als Massepunkte betrachtet, die eine gleichförmige Bewegung ausführen. Als Beginn der Betrachtungen wird der Zeitpunkt t = 0 s gewählt. Zu diesem Zeitpunkt befindet sich der Radfahrer 100 m vor dem Pkw. Diese Strecke wird als bereits zurückgelegter Weg angenommen, während dem Pkw für diesen Zeitpunkt der Weg null zugeordnet wird.
| Gesucht: | t |
| Gegeben: |
Lösung:
Für die grafische Lösung wird werden die Bewegungen von Radfahrer und Pkw in einem s-t-Diagramm dargestellt. Für beide gilt das Weg-Zeit-Gesetz in der Form .
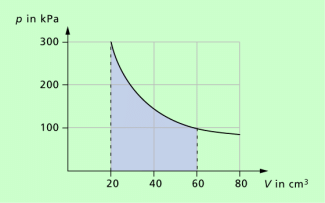
Bild 1 zeigt die entsprechende grafische Darstellung.
Der Schnittpunkt beider Geraden ist der Punkt, an dem der Pkw den Radfahrer eingeholt hat. Aus dem Diagramm kann man ablesen: Bis zum Einholen des Radfahrers vergeht eine Zeit von 20 s. Während dieser Zeit legt der Radfahrer einen Weg von 100 m und der Pkw einen Weg von 200 m zurück.
Ergebnis:
Geht man von dem Zeitpunkt aus, an dem sich der Pkw 100 m hinter dem Radfahrer befindet, so braucht der PKkw bis zum Einholen des Radfahrers 20 s und legt dabei einen Weg von 200 m zurück. In der gleichen Zeit fährt der Radfahrer 100 m.
Hinweis:
Die Aufgabe kann auch gelöst werden, indem man für beide Bewegungen das jeweilige Weg-Zeit-Gesetz aufstellt und daraus zunächst die Zeit ermittelt, zu der sich beide Körper treffen. Aus dieser Zeit können den die bis dahin zurückgelegten Wege berechnet werden.
Weg-Zeit-Diagramm für zwei verschiedene gleichförmige Bewegungen
Beispiel 2:
Die Luft in einem Zylinder wird durch Verschieben eines Kolbens zusammengedrückt. Für Volumen und Druck ergeben sich folgende Werte:
| 80 | 60 | 40 | 20 | |
| Druck in kPa | 75 | 100 | 170 | 300 |
a) Zeichnen Sie das Druck-Volumen-Diagramm für diesen Vorgang!
b) Ermitteln Sie aus dem Diagramm die Arbeit, die erforderlich ist, um die Luft im Zylinder von zu komprimieren!
Lösung:
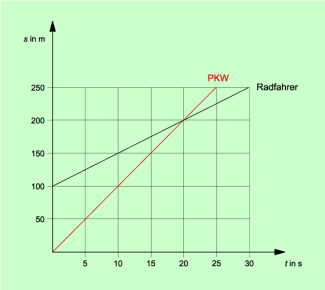
Bild 2 zeigt das entsprechende p-V-Diagramm. In einem solchen Diagramm ist die Fläche unter dem Graphen gleich der verrichteten Volumenarbeit. Diese Fläche kann durch Auszählen ermitteln werden, wobei die Einheiten zu beachten sind. Für den gegebenen Fall erhält man:
Unter der Annahme der Gültigkeit des Druck-Volumen Gesetzes lässt sich die Volumenarbeit auch mithilfe der Integralrechnung ermitteln.
p-V-Diagramm für die Kompression von Luft: Das Diagramm ergibt sich aus den angegebenen Messwerten.
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 