Magnetische Flussdichte und magnetische Feldstärke

Ein magnetisches Feld kann man mit dem Modell Feldlinienbild kennzeichnen. Quantitativ lässt es sich durch die feldbeschreibenden Größen magnetische Flussdichte und magnetische Feldstärke charakterisieren. Die magnetische Flussdichte B, die heute vorzugsweise verwendet wird, ist folgendermaßen definiert:
$B = \frac{F}{Ι \cdot l}$
Die magnetische Feldstärke H ist mit der magnetischen Flussdichte folgendermaßen verknüpft:
$B = μ_{0} \cdot μ_{r} \cdot H$

Induktion

#Induktion #Lorentzkraft #Bewegte Ladung #Induktionsspannung #Induktionsstrom

Induktionsspule

#Induktion #Lorentzkraft #Bewegte Ladung #Induktionsspannung

Ähnlich wie beim elektrischen Feld verwendet man heute vorzugsweise eine der beiden Größen. Während beim elektrischen Feld vorrangig die elektrische Feldstärke genutzt wird, ist beim magnetischen Feld die magnetische Flussdichte die bevorzugte Größe.

Magnetische Flussdichte

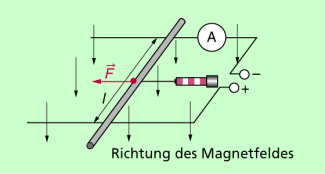
Auf einen stromdurchflossenen Leiter im Magnetfeld wird eine Kraft ausgeübt. Diese Kraft hängt bei einer konstanten Stärke des magnetischen Feldes und bei einer bestimmten Länge des Leiters im Feld nur von der Stärke des Feldes selbst ab. Die Richtung der Kraft ist senkrecht zur Richtung des magnetischen Feldes und senkrecht zur Stromrichtung.

Genauer kann man die Zusammenhänge mit einer einfachen Versuchsanordnung untersuchen, die in Bild 2 dargestellt ist. Es wird die Abhängigkeit der Kraft F von verschiedenen Parametern erfasst. Der Leiter befindet sich senkrecht zu den Feldlinien des Magnetfeldes. Führt man die Untersuchungen durch, dann zeigt sich:

Bei konstanter Länge l ist die Kraft F auf den Leiter in einem homogenen Magnetfeld umso größer, je größer die Stromstärke I im Leiter ist. Es gilt:
$F \sim Ι$
Bei konstanter Stromstärke ist die Kraft F auf den stromdurchflossenen Leiter umso größer, je größer die Länge l ist, die sich im Magnetfeld befindet. Es gilt:
$F \sim l$
Fasst man diese beiden Proportionalitäten zusammen, so erhält man für ein Magnetfeld bestimmter Stärke:
$F \sim Ι \cdot l oder \frac{F}{Ι \cdot l} = konstant$

Weitere Untersuchungen zeigen: In einem stärkeren Magnetfeld ist der Quotient größer, in einem schwächeren kleiner. Er ist somit geeignet, die Stärke eines Magnetfeldes zu kennzeichnen. Aus historischen Gründen bezeichnet man diesen Quotienten als magnetische Flussdichte oder auch als magnetische Induktion und definiert:
Unter der Bedingung, dass sich ein stromdurchflossener Leiter senkrecht zu den Feldlinien eines Magnetfeldes befindet, kann die magnetische Flussdichte ermittelt werden mit der Gleichung:

$\begin{array}{l} B = \frac{F}{Ι \cdot l} \\ F Kraft auf den stromdurchflossenen Leiter \\ Ι Stromstärke im Leiter \\ l Länge des Leiters \end{array}$
Gemessen wird die magnetische Flussdichte in der Einheit ein Tesla (1 T), benannt nach dem kroatisch-amerikanischen Elektrotechniker und Physiker NICOLA TESLA (1856-1943). Für die Einheit gilt:
$1 T = 1 \frac{N}{m \cdot A} = 1 \frac{V \cdot s}{m^{2}} = 1 \frac{Wb}{m^{2}}$
Befindet sich der stromdurchflossene Leiter nicht senkrecht zu den Feldlinien, dann gilt:
$\begin{array}{l} F = Ι \cdot l \cdot B \cdot \sin ∢ (B, Ι) oder vektoriell \\ \vec{F} = l (\vec{Ι} \times \vec{B}) \end{array}$
Die magnetische Flussdichte ist eine vektorielle Größe, die die gleiche Richtung wie die Feldlinien hat. Sie steht senkrecht zur Stromstärke und senkrecht zur Kraft.

Magnetische Feldstärke

Die zweite feldbeschreibende Größe für das Magnetfeld ist die magnetische Feldstärke. Dabei geht man davon aus, dass die Stärke des Feldes durch die Wirkung bestimmt werden kann, die das Feld auf einen in ihm befindlichen Probemagneten ausübt. Da Pole nicht isoliert, sondern nur paarweise vorkommen, erfahren Nord- und Südpol des Probemagneten entgegengesetzte Kraftwirkungen. Es entsteht ein Drehmoment, das einen drehbar gelagerten Probemagneten in Feldrichtung bewegt. Dieses Drehmoment ist ein Maß für die magnetische Feldstärke an der betreffenden Stelle. Auch die magnetische Feldstärke ist eine vektorielle Größe, die die gleiche Richtung wie die Feldlinien und damit auch die gleiche Richtung wie die magnetische Flussdichte hat. Sie wird in der Einheit A/m gemessen.

Zusammenhang zwischen der magnetischen Flussdichte und der magnetischen Feldstärke

Da ein magnetisches Feld durch beide Größen gekennzeichnet werden kann, können sich die Größen nur durch eine Konstante voneinander unterscheiden. Es gilt folgender Zusammenhang:
$\begin{array}{l} \vec{B} = μ_{0} \cdot μ_{r} \cdot \vec{H} \\ B magnetische Flussdichte \\ μ_{0} magnetische Feldkonstante \\ μ_{r} Permeabilitätszahl \\ H magnetische Feldstärke \end{array}$

Magnetische Flussdichte und magnetische Feldstärke von speziellen Feldern

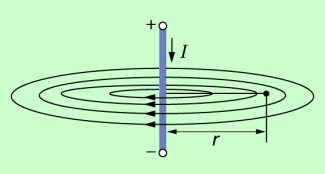
Ein stromdurchflossener Leiter ist von einem Magnetfeld umgeben (Bild 3). Für das Feld eines geraden, stromdurchflossenen Leiters in der Entfernung r gilt:
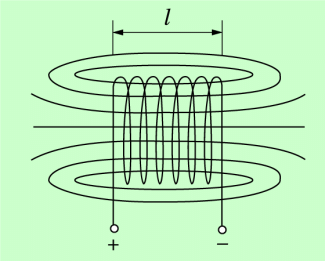
$\begin{array}{l} B = μ_{0} \cdot μ_{r} \cdot \frac{Ι}{2 π \cdot r} oder H = \frac{Ι}{2 π \cdot r} \\ B magnetische Flussdichte \\ H magnetische Feldstärke \\ μ_{0} magnetische Feldkonstante \\ μ_{r} Permeabilitätszahl \\ Ι Stromstärke im Leiter \\ r Abstand vom Leiter \end{array}$

Für das weitgehend homogene Feld im Inneren einer langen stromdurchflossenen Spule gilt:
$\begin{array}{l} B = μ_{0} \cdot μ_{r} \cdot \frac{N \cdot Ι}{l} oder H = \frac{N \cdot Ι}{l} \\ B magnetische Flussdichte \\ H magnetische Feldstärke \\ μ_{0} magnetische Feldkonstante \\ μ_{r} Permeabilitätszahl \\ N Windungszahl der Spule \\ Ι Stromstärke durch die Spule \\ l Länge der Spule \end{array}$

Der Term $μ_{0} \cdot μ_{r}$ wird auch als Permeabilität $μ$ bezeichnet. Damit kann man die Gleichungen für die magnetische Flussdichte etwas einfacher schreiben.

Material zum Thema

BWS-PHY2-0394-12.mcd

BWS-PHY2-0394-12.mcd

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel