Potenzielle Energie und Potenzial
Potenzielle Energie und Potenzial sind wichtige Größen zur Charakterisierung eines Gravitationsfeldes.
Die potenzielle Energie eines Körpers ist von der Stärke des Gravitationsfeldes, von seiner Masse und davon abhängig, auf welches Bezugsniveau man die potenzieller Energie bezieht. In der Physik ist es üblich, die potenzielle Energie im Unendlichen null zu setzen.
Das Potenzial charakterisiert das Feld und ist damit eine Feldgröße. Unter dem Potenzial eines Punktes im Gravitationsfeld versteht man einen Zustand des Feldes, der ein Maß für die potenzielle Energie eines Körpers im betreffenden Punkt ist, wobei als Bezugspunkt (Nullniveau) ein Punkt im Unendlichen gewählt wird.
Die potenzielle Energie
Allgemein ist die potenzielle Energie eines Körpers von der Stärke des Gravitationsfeldes, von seiner Masse und davon abhängig, auf welches Bezugsniveau man die potenzieller Energie bezieht. Sie ist zugleich ein Maß für sein Arbeitsvermögen. Im oberflächennahen Gravitationsfeld, also in unserem Lebensbereich bis etwa 10 km Höhe über NN, kann das Gravitationsfeld als homogen angesehen werden.
Für diesen Bereich bezieht man die potenzielle Energie häufig auf die Erdoberfläche und setzt die potenzielle Energie für dieses Bezugsniveau null. Dann ist die potenzielle Energie in einer Höhe h genauso groß wie die Hubarbeit, die zum Heben des Körpers auf diese Höhe erforderlich ist. Es gilt:
Es kann auch ein beliebiges anderes Bezugsniveau gewählt werden. An der Art der Berechnung der potenziellen Energie ändert sich dadurch nichts.
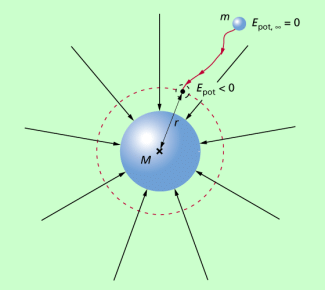
Für größere Raumbereiche ist zu beachten, dass das Gravitationsfeld nicht homogen ist und somit ein anderes Herangehen erforderlich ist. Darüber hinaus ist es in der Physik üblich, das Nullniveau ins Unendliche zu legen. Dann ist die potenzielle Energie eines Körpers in einem beliebigen Punkt gleich der Arbeit, die verrichtet werden muss, um den Körper aus dem Unendlichen bis zu diesem Punkt zu verschieben (Bild 1). Damit gilt:
Dabei bedeuten G die Gravitationskonstante, M die Masse des felderzeugenden Körpers, m die Masse des im Feld befindlichen Körpers und r der Abstand zwischen dem Massenmittelpunkt des felderzeugenden Körpers und des Körpers mit der Masse m.
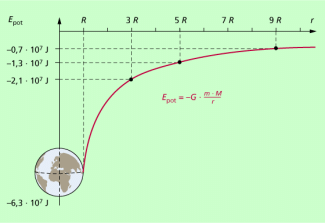
Das bedeutet, dass die potenzielle Energie eines beliebigen Punktes eines Gravitationsfeldes negativ ist und ihren größten (negativen) Wert in der Entfernung R hat, wobei R der Radius des felderzeugenden Körpers ist (Bild 2). Für das Gravitationsfeld der Erde bedeutet das: Ein Körper der Masse 1 kg hat auf der Erdoberfläche folgende potenzielle Energie:
Mit Entfernung von der Erdoberfläche vergrößert sich die potenzielle Energie und erreicht im Unendlichen den Wert null (Bild 2).
Das Potenzial
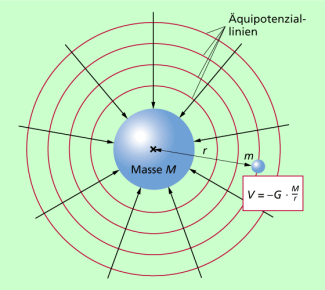
Um ein Gravitationsfeld um einen Körper der Masse M unabhängig von Körpern beschreiben zu können, die sich in diesem Feld befinden, führt man die Größe Potenzial ein. Die Bezeichnung "Potential" (neue Schreibweise: Potenzial) wurde 1836 von CARL FRIEDRICH GAUSS (1777-1855) in die Wissenschaft eingeführt.
Das Potenzial eines Punktes im Gravitationsfeld eines felderzeugenden Körpers ist ein Maß für die potenzielle Energie, die ein im Feld befindlicher Körper haben würde.
Formelzeichen: V
Einheit: ein Joule durch Kilogramm
Das Potenzial in einem Gravitationsfeld kann berechnet werden mit der Gleichung:
Aus dem Vergleich mit der potenziellen Energie kann man erkennen: Das Potenzial beträgt für die Erdoberfläche:
Mit zunehmender Entfernung vom felderzeugenden Körper vergrößert es sich und erreicht im Unendlichen den Wert null.