Schweredruck in Flüssigkeiten

Ein Druck tritt auf, wenn ein Körper mit einer Kraft auf eine Fläche wirkt. Diese Kraft kann auch die Gewichtskraft einer Flüssigkeitssäule sein.
Den Druck in einer Flüssigkeit, der infolge der Gewichtskraft einer darüber liegenden Flüssigkeitssäule entsteht, nennt man Schweredruck.

Der Schweredruck ist ein spezieller Druck. Es gelten für ihn aber alle Aussagen, die für den Druck allgemein zutreffen. Insbesondere ist der Schweredruck in einer bestimmten Tiefe in allen Richtungen gleich groß.

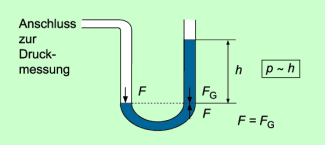
Verdeutlichen kann man sich das Zustandekommen des Schweredrucks anhand einer Skizze (Bild 2): Befindet man sich in einer Flüssigkeit, z. B. in Wasser, in einer bestimmten Tiefe, so wirkt an dieser Stelle auf eine Fläche A die Gewichtskraft der darüber liegenden Flüssigkeitssäule. Die Kraft je Fläche ist gleich dem Druck, den die Flüssigkeitssäule ausübt.

Berechnen des Schweredrucks

Der Schweredruck in einer Flüssigkeit ist abhängig

• von der Eintauchtiefe in die Flüssigkeit und
• von der Art und somit der Dichte der Flüssigkeit.

Er ist umso größer, je tiefer man in die Flüssigkeit eintaucht und je größer die Dichte der Flüssigkeit ist. Es gilt wie für jeden Druck:

$\begin{array}{l}p=\frac{F}{A}\\ \text{Setzt man für die Kraft die Gewichtskraft}{F}_G\text{der}\\ \text{Flüssigkeitssäule ein}\text{, so erhält man mit}{F}_G=m\cdot g\\ p=\frac{F_G}{A}=\frac{m\cdot g}{A}\end{array}$

Setzt man für die Masse das Produkt aus Dichte und Volumen und für das Volumen wiederum das Produkt aus Fläche der Flüssigkeitssäule und ihrer Höhe, so erhält man:

$\begin{array}{l}p=\frac{m\cdot g}{A}=\frac{\rho \cdot V\cdot g}{A}=\frac{\rho \cdot A\cdot h\cdot g}{A}\\ \text{Durch Kürzen von}A\text{erhält man für den Schweredruck}\\ \text{die Gleichung}\\ p=\rho \cdot h\cdot g\\ \rho \text{Dichte der Flüssigkeit}\\ h\text{Höhe der Flüssigkeitssäule (Eintauchtiefe)}\\ g\text{Fallbeschleunigung}\end{array}$

Beachte: Setzt man die Dichte in ${\text{g/cm}}^{\text{3}}$ , die Höhe in cm und die Fallbeschleunigung in ${\text{cm/s}}^{\text{2}}{\text{(981 cm/s}}^{\text{2}})$ ein, so erhält man als Einheit:

$\frac{\text{g}}{\text{cm}\cdot {\text{s}}^{\text{2}}}$

Es gilt:

$\begin{array}{l}1\frac{\text{g}}{\text{cm}\cdot {\text{s}}^{\text{2}}}=\frac{1}{10}\frac{\text{kg}}{\text{m}\cdot {\text{s}}^{\text{2}}}\\ \text{Erweitert man den rechts stehenden Ausdruck mit 1}\text{m}\text{,}\\ \text{so erhält man:}\\ \text{1}\frac{\text{g}}{\text{cm}\cdot {\text{s}}^{\text{2}}}=\frac{1}{10}\frac{\text{kg}\cdot \text{m}}{{\text{m}}^{\text{2}}\cdot {\text{s}}^{\text{2}}}=\frac{1}{10}\frac{\text{N}}{{\text{m}}^{\text{2}}}=\frac{1}{10}\text{Pa}\end{array}$

Schweredruck in Wasser

Der Schweredruck in Wasser spielt eine besondere Rolle, weil Wasser in Natur und Technik die am weitesten verbreitete Flüssigkeit ist. Für Wasser kann man den Schweredruck in einer bestimmten Tiefe mithilfe der oben genannten Gleichungen berechnen. Führt man diese Berechnung für verschiedene Wassertiefen durch, dann ergibt sich:

In Wasser nimmt der Schweredruck je 10 Meter Tiefe um etwa 100 kPa zu.

Aus einem p-h-Diagramm kann man leicht ablesen, welcher Druck in welcher Tiefe herrscht. Taucht man z. B. beim Baden in eine Tiefe von
1 m, so beträgt der Schweredruck in dieser Tiefe 10 kPa. In 100 m Wassertiefe beträgt der Schweredruck bereits 1.000 kPa = 1 MPa. Das ist ein Druck, in dem ein Mensch nicht mehr leben kann. Beim Tauchen in solche Tiefen ist eine spezielle Tiefseeausrüstung erforderlich.

Die größte Meerestiefe erreichten 1960 die beiden Forscher PICCARD und WALSH mit einer Tauchkugel, die eine Außenwand aus Stahl mit einer Wandstärke von 12 cm und kleine Fenster mit einer Wandstärke von 15 cm hatte. Diese starken Wände und Scheiben waren notwendig, weil in der erreichten Tiefe von ca. 11.000 m ein Schweredruck des Wasser von 110 MPa herrscht und durch einen solchen Druck eine dünnwandige Kugel zerdrückt werden würde.

Das hydrostatische Paradoxon

Der Schweredruck in einer Flüssigkeit ist zwar abhängig von der Eintauchtiefe und von der Dichte der Flüssigkeit, nicht aber von der Form des Gefäßes. Dies führt zu einer Reihe von sonderbaren (paradoxen) Erscheinungen und wird deshalb als hydrostatisches Paradoxon bezeichnet. Eine dieser paradoxen Erscheinungen kann man experimentell einfach demonstrieren: Man füllt in Gefäße unterschiedlicher Form Wasser und wählt die Füllhöhe überall gleich groß. Die Flächen am unteren Rand der Gefäße sind überall gleich groß. Dann ist die Annahme naheliegend, dass der Schweredruck am Boden des Gefäßes mit dem meisten Wasser am größten ist. Messungen zeigen aber: Der Schweredruck am Boden ist bei allen Gefäßen gleich groß.