Stehende Wellen
Wellen breiten sich von einem Erreger aus in den Raum hinein aus. Man spricht deshalb manchmal auch von fortschreitenden Wellen. Werden sie an Hindernissen reflektiert, so können sich die hin- und rücklaufenden Wellen überlagern. Es kommt zur Ausbildung einer stehenden Welle, bei der sich Schwingungsknoten und Schwingungsbäuche stets an der gleichen Stellen befinden.
Dies kann an einer Saite, die zu Schwingungen angeregt wird gezeigt werden. Im Schwingungsknoten ruht die Saite, im Schwingungsbauch hat sie ihre maximale Auslenkung. Schwingungsknoten und Schwingungsbäuche befinden sich stets an der gleichen Stelle. Der Abstand zweier benachbarter Schwingungsknoten oder Schwingungsbäuche ist gleich der halben Wellenlänge.
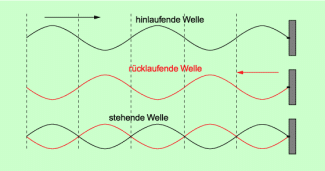
In Bild 2 ist erkennbar, wie eine stehende Welle entsteht: Hinlaufende und rücklaufende Welle überlagern sich und bilden gemeinsam die stehende Welle. Man kann eine solche stehende Welle auch erzeugen, wenn man ein Seil an einem Haken befestigt und das andere Ende des Seils mit der Hand in Schwingungen versetzt. Die erforderliche Frequenz muss man ausprobieren.
Dabei ist zu beachten, ob die Enden fest eingespannt oder lose sind. Bei der Reflexion am festen Ende tritt ein Phasensprung auf; hin- und rücklaufende Welle haben entgegengesetzte Phase. Bei der Reflexion tritt keine Phasenverschiebung auf, hin- und rücklaufende Welle haben gleiche Phase.
-
Entstehung stehender Wellen: Dargestellt ist der Fall, dass beide Enden fest eingespannt sind (Reflexion am festen Ende).
Nutzen kann man stehende Wellen z.B. zur Bestimmung der Wellenlänge von Schallwellen. Dazu wird ein beidseitig offenes Glasrohr in Wasser getaucht und über dem Glasrohr ein Lautsprecher angebracht, der mit einem Tonfrequenzgenerator verbunden ist. Die vom Lautsprecher ausgehenden Schallwellen werden an der Wasseroberfläche reflektiert. Dort befindet sich stets ein Schwingungsknoten. Beträgt die Länge der Luftsäule gerade ein Viertel der Wellenlänge, so befindet sich am Ende des Glasrohres ein Schwingungsbauch, erkennbar an der besonders großen Lautstärke. Ein Schwingungsbauch tritt ebenfalls auf, wenn die Länge der Luftsäule drei Viertel der Wellenlänge beträgt. Damit gilt:
Kennt man die Frequenz der Schallwellen, dann kann man mithilfe der Gleichung
die Schallgeschwindigkeit berechnen.
Stehende Wellen bei Platten
Stehende Wellen bilden sich auch bei schwingenden Platten aus. Um sich das zu veranschaulichen, wird z. B. feiner Sand gleichmäßig auf eine Platte gestreut und diese Platte in Schwingungen bestimmter Frequenz versetzt. Es bilden sich dann charakteristische Strukturen aus, so wie sie in Bild 4 zu sehen sind. Der Sand sammelt sich in den Schwingungsknoten. Diese Strukturen werden als chladnische Klangfiguren bezeichnet, benannt nach dem deutschen Juristen und Akustiker ERNST FLORENS FRIEDRICH CHLADNI (1756-1827), der diese Strukturen am Beispiel von Schallwellen erstmals genauer untersucht hat. Die Form der Figuren hängt von der Form der Platte und von der Erregerfrequenz ab.

