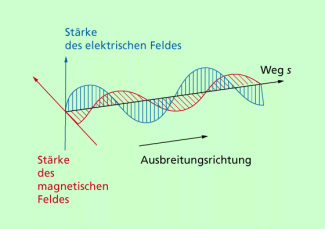
Ausbreitungsgeschwindigkeit

Für die Erkenntnis, dass alle elektromagnetischen Wellen von gleicher physikalischer Beschaffenheit sind, ist ihre einheitliche Ausbreitungsgeschwindigkeit von etwa 300 000 km/s im Vakuum von großer Bedeutung. Mit dieser Geschwindigkeit pflanzen sich zum Beispiel Lichtwellen, Röntgenwellen, aber auch Radiowellen durch den Raum hindurch fort.

In den Jahren 1868/69 berechnete der englische Physiker JAMES CLERK MAXWELL (1831-1879), dass sich elektromagnetische Wellen exakt mit Lichtgeschwindigkeit ausbreiten. Diese Übereinstimmung mit der Fortpflanzungsgeschwindigkeit des Lichtes konnte nicht als zufälliger Effekt abgetan werden.

Nachdem HEINRICH HERTZ (1857-1894) die hertzschen Wellen entdeckt und ihre Ausbreitung experimentell untersucht hatte, wurde allmählich zur Gewissheit, dass hertzsche Wellen sich physikalisch ähnlich wie Lichtwellen verhalten. Auch die in den darauffolgenden Jahren entdeckten Röntgenstrahlen und die Gammastrahlen besitzen alle eine übereinstimmende Vakuumlichtgeschwindigkeit und sind demzufolge elektromagnetische Wellen.

Wie bei anderen Wellen besteht zwischen der Ausbreitungsgeschwindigkeit, der Wellenlänge und der Frequenz folgender Zusammenhang:

$\begin{array}{l}c=f\cdot \lambda \\ c\text{ Ausbreitungsgeschwindigkeit}\\ f\text{ Frequenz}\\ \lambda \text{ Wellenlänge}\end{array}$

Die Lichtgeschwindigkeit - und damit die Ausbreitungsgeschwindigkeit aller elektromagnetischer Wellen im Vakuum - kann auch mithilfe folgender Gleichung berechnet werden:

$c=\frac{1}{\sqrt{{\epsilon }_0\cdot {\mu }_0}}$

In dieser Gleichung bedeuten ${\epsilon }_0$die elektrische Feldkonstante und ${\mu }_0$die magnetische Feldkonstante. Da es sich bei diesen beiden Größen um Naturkonstanten handelt und da sie als alleinige Berechnungsgrößen zur Ermittlung der Lichtgeschwindigkeit herangezogen werden, folgt, dass auch die Lichtgeschwindigkeit eine Naturkonstante sein muss. Diese Erkenntnis war ein wichtiger Ausgangspunkt zur Formulierung der speziellen Relativitätstheorie.