Ballistische Kurven

Bei der Überlagerung einer gleichförmigen Bewegung unter einem Winkel zur Waagerechten und des freien Falls in senkrechter Richtung, also bei einem schrägen Wurf, entsteht als Bahnkurve eine Wurfparabel, wenn der Luftwiderstand vernachlässigt werden kann. Kennzeichnend für eine solche Wurfparabel ist der spiegelsymmetrische Verlauf.
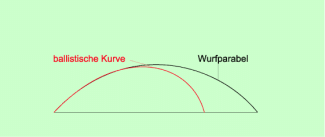
Bei vielen Bewegungen beeinflusst der Luftwiderstand den Bahnverlauf. Damit entstehen Kurven, die von der Idealform einer Wurfparabel abweichen und als ballistische Kurven bezeichnet werden. Die Wurfweite ist bei gleicher Anfangsgeschwindigkeit geringer als bei Wurfparabeln.

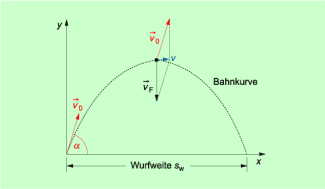
Bei einem schrägen Wurf überlagern sich eine gleichförmige geradlinige Bewegung unter einem Winkel zur Waagerechten und eine gleichmäßig beschleunigte Bewegung - der freie Fall - in senkrechter Richtung. Wurfhöhe und Wurfweite sind abhängig

von der Abwurfgeschwindigkeit und
vom Abwurfwinkel.

Die größte Wurfweite wird bei der ungestörten Bewegung eines Körpers und einem Abwurfwinkel von 45° erreicht. Reine Wurfparabeln treten nur bei Bewegungen im Vakuum auf.

Die Bahnkurve ergibt sich aus den beiden Teilbewegungen (Bild 2). Die Gleichung für die Wurfparabel lautet:

$y = \tan α \cdot x - \frac{g}{2 v_{0}^{2} \cdot \cos^{2} α} \cdot x^{2}$

Die Bahnkurve beim schrägen Wurf ist eine Parabel (Wurfparabel)

Wenn man z. B. die Bahn eines Fußballs, eines Speers oder eines Geschosses verfolgt, dann stellt man fest, dass die Bahnen dieser Körper in der Regel erheblich von der Wurfparabel abweichen. Man nennt eine solche Bahn eine ballistische Kurve (Bild 3). Die Lehre von den Flugbahnen von Körpern (Geschossen) wird als Ballistik bezeichnet.

Ursache für das Entstehen solcher ballistischer Kurven ist das Wirken des Luftwiderstandes, der entgegen der Bewegungsrichtung des Körpers wirkt und damit die Bewegung behindert.
Bei Geschossen und auch bei vielen Würfen im Sport (Speerwerfen, Bewegung von Fußbällen und Golfbällen) sind die Bahnkurven ballistische Kurven, weil die Bewegung der Körper erheblich durch den Luftwiderstand beeinflusst wird. Die Wurfweite ist in allen diesen Fällen wesentlich geringer als die Wurfweiten, die man mithilfe der Gesetze des schrägen Wurfes berechnen würde.

Wurfparabel und ballistische Kurve

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Kostenlos ausprobieren

Verwandte Artikel

Ballistische Kurven

Rechtliches

Einloggen