Energie des elektrischen Feldes
Die bei einer Ladungstrennung aufgewandte Arbeit ist als Energie im elektrischen Feld zwischen den Ladungen gespeichert. Diese elektrische Feldenergie bezeichnet man häufig auch kurz als elektrische Energie.
| Formelzeichen: Einheiten: | 1 Wattsekunde (1 ) oder 1 Joule (1 J) |
Die bei einer Ladungstrennung aufgewandte Arbeit ist als Energie im elektrischen Feld zwischen den Ladungen gespeichert. Diese elektrische Feldenergie bezeichnet man häufig auch kurz als elektrische Energie.
| Formelzeichen: Einheiten: |
|
Die Berechnung der elektrischen Energie
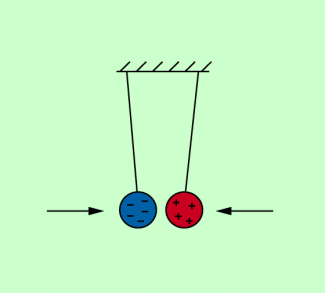
Hat man mechanische Arbeit aufgewandt, um ungleichnamige Ladungen zu trennen, dann sind diese Ladungsträger bei ihrer Zusammenführung nun ihrerseits in der Lage, eine Arbeit zu verrichten. Zwei ungleichnamig geladene Kugeln können zum Beispiel mechanische Arbeit verrichten, wenn sie sich aus größerer Entfernung aufeinander zu bewegen und beim Aufprall verformen.
Zur Berechnung der elektrischen Energie geht man von der Arbeit aus, die zur Ladungstrennung erforderlich ist. Nach dem Energieerhaltungssatz ist diese Arbeit genau so groß, wie die im elektrischen Feld gespeicherte Energie.
-
elektrostatische Anziehung
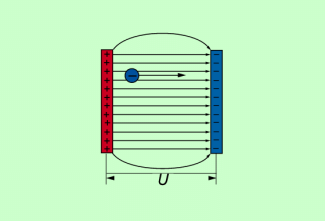
Für den Plattenkondensator ist die Berechnung der elektrischen Energie besonders einfach.
Um im Kondensator ein elektrisches Feld aufzubauen, muss man einer Kondensatorplatte nacheinander Elementarladungen e entnehmen und auf die andere Platte verschieben.
Für die Verschiebungsarbeit einer Ladung e zwischen zwei Kondensatorplatten gilt:
Allerdings ist bei der Berechnung folgender Umstand zu berücksichtigen:
Da der Kondensator im Ausgangszustand noch gar nicht geladen ist, beträgt die Spannung zwischen den Platten bei der ersten Ladungsverschiebung U=0 und demzufolge auch die elektrische Arbeit W=0. Erst wenn man die letzte Ladung e auf die andere Kondensatorplatte bringt, hat sich zwischen den Platten fast schon die volle Spannung U aufgebaut. Dies bedeutet: Für die Berechnung der gesamten Verschiebungsarbeit, darf man nicht die obige Gleichung verwenden, sondern muss von der mittleren Verschiebungsarbeit der Ladungen ausgehen. Diese ist aus dem Mittelwert aller Einzelverschiebungen zu berechnen. Dieser Mittelwert beträgt:
Die Gesamtarbeit und damit auch die Energie des elektrischen Feldes ist die Summe aller Einzelverschiebungen:
Ersetzt man in der Berechnungsgleichung die Ladung der Kondensatorplatten durch ihre elektrische Kapazität, dann gilt für die Feldenergie:
Diese Gleichung gilt für beliebige Formen von Kondensatoren.
-
Ladungsverschiebung zwischen zwei Kondensatorplatten