Fehlerbetrachtungen
Jede Messung einer physikalischen Größe ist aus den verschiedensten Gründen mit Fehlern behaftet. Um möglichst genaue Messungen durchführen zu können bzw. um die Genauigkeit bereits durchgeführter Messungen einschätzen zu können, muss man die Ursachen für Messfehler, die Größen solcher Fehler und ihre Auswirkungen auf die Genauigkeit des Ergebnisses kennen.
Fehler bei physikalischen Messungen
Jede Messung einer physikalischen Größe ist aus den verschiedensten Gründen mit Fehlern behaftet. Der Messwert einer physikalischen Größe weicht also vom tatsächlichen Wert der Größe, wahrer Wert x genannt, mehr oder weniger stark ab. Um möglichst genaue Messungen durchführen zu können bzw. um die Genauigkeit bereits durchgeführter Messungen einschätzen zu können, muss man die Ursachen für Messfehler, die Größen solcher Fehler und ihre Auswirkungen auf die Genauigkeit des Ergebnisses kennen. Darüber hinaus muss man wissen, wie man in der Formulierung des Ergebnisses die Genauigkeit kenntlich macht.
| Jede Messung ist mit Fehlern behaftet. Die Messwerte weichen vom wahren Wert x der betreffenden Größe ab. |
Ursachen für Messfehler
Messfehler können ihre Ursachen haben
- in der Experimentieranordnung,
- in den Messgeräten bzw. Messmitteln,
- beim Experimentator,
- in der Umgebung, in der das Experiment (die Messung) durchgeführt wird.
Es spielen also sowohl objektive und vom Experimentator nicht zu beeinflussende als auch subjektive und beeinflussbare Faktoren eine Rolle.
In der nachfolgenden Übersicht sind einige Beispiele für Fehlerursachen genannt.
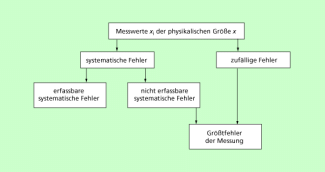
Aus der Übersicht ist ersichtlich, dass es bei jedem Experiment zahlreiche Fehlerursachen und damit auch viele mögliche Fehler gibt. Eine genauere Analyse zeigt, dass man alle diese Fehler zu wenigen Fehlerarten zusammenfassen kann (Bild 2).
-
Freier Fall

| Fehlerursache | Beispiele |
| Experimentieranordnung |
|
| Messgeräte, Messmittel |
|
| Experimentator |
|
| Umgebung |
|
Arten von Messfehlern
Je nach ihrem Charakter unterscheidet man zwischen groben, systematischen und zufälligen Fehlern (Bild 2).
Grobe Fehler sind Fehler, die aufgrund eines falschen Aufbaus, ungeeigneter Messgeräte, falschen Ablesens, defekter Messgeräte oder Unachtsamkeit auftreten. Bei sorgfältiger und planmäßiger Arbeit sind grobe Fehler grundsätzlich vermeidbar. Sie werden deshalb bei Fehlerbetrachtungen nicht berücksichtigt. Tritt ein grober Fehler auf, so sind die entsprechenden Werte zu streichen und die Messungen zu wiederholen.
Systematische Fehler sind Fehler, die vor allem durch die Experimentieranordnung oder durch die Messgeräte verursacht werden, aber auch vom Experimentator selbst hervorgerufen werden können. Sie treten, wie schon der Name sagt, nicht zufällig auf, sondern sind durch die Art und Weise der Messungen bestimmt und wirken sich auch meist in gleicher Weise aus, wenn die Messungen mehrmals durchgeführt werden. Systematische Fehler können teilweise erfasst und korrigiert werden. So können z. B. die Fehler, die durch Wärmeverluste bei der Mischung zweier Flüssigkeiten verschiedener Temperatur auftreten, gering gehalten werden, wenn man die Wärme mit berücksichtigt, die vom Gefäß aufgenommen oder abgegeben wird (Wärmekapazität des Kalorimeters).
| Messgerät | maximaler systematischer Fehler |
Thermometer
| ± 1 K |
| Lineal, Winkelmesser, Messuhren, Uhren, Präzisionswaagen | ± 1 % (meist vernachlässigbar) |
| Brennweite von Linsen, Gitterkonstante eines optischen Gitters | ± 1 % (meist vernachlässigbar) |
| Federkraftmesser | meist Genauigkeitsklasse 2,0 |
| Spannungsmesser Stromstärkemesser Widerstandsmesser | aufgedruckte Genauigkeitsklasse (sie bezieht sich immer auf den jeweiligen Messbereichsendwert) |
Systematische Fehler kommen auch durch die Ungenauigkeit der Messgeräte zustande. Diese Fehler werden über die Genauigkeitsklasse oder die Toleranz der betreffenden Geräte erfasst. Diese sind zumeist in den Betriebsanleitungen angegeben.
So bedeutet z. B. bei einem Spannungsmesser die Genauigkeitsklasse 2,5 bei einem Messbereich von 10 V: Der maximale systematische Fehler beträgt bei allen Messungen in diesem Messbereich 2,5 % vom Messbereichsendwert, also 2,5 % von 10 V und damit ± 0,25 V. Entsprechend lassen sich auch für andere Messgeräte die maximalen systematischen Fehler angeben (s. Übersicht).
Zufällige Fehler sind Fehler, die vor allem durch den Experimentator und durch Umwelteinflüsse zustande kommen. Dazu gehören z. B. Ablesefehler bei Messgeräten, Ablesefehler bei Zeitmessungen, ungenaues Einstellen der Schärfe eines Bildes in der Optik u. Ä.
| Art des zufälligen Fehlers | Größe des zufälligen Fehlers |
| Ungenaues Ablesen bei Messgeräten mit analoger Anzeige (Skalen) | Hälfte des kleinsten Skalenwertes (z. B. bei einem Lineal mit mm-Teilung: ± 0,5 mm, bei einem Thermometer mit 1/2 °-Teilung: ± 0,25 K) |
| Ungenauigkeit bei Messgeräten mit digitaler Anzeige (Ziffern) | Abweichung um 1 von der letzten Ziffer (z. B. bei einem elektronischen Thermometer mit der Anzeige 22,8 °C ± 0,1 K) |
| Auslösefehler bei handgestoppten Zeitmessungen | ± 0,25 s (Mittelwert) |
Solche zufälligen Fehler lassen sich teilweise abschätzen, aber nie vollständig erfassen. Für einige zufällige Fehler sind in der vorhergegangenen Übersicht Werte angegeben. Zufällige Fehler haben statistischen Charakter. Bei mehrfacher Messung streuen sie um einen Mittelwert.
Bei Messungen können sowohl systematische als auch zufällige Fehler auftreten. Die Summe aller Fehler ergibt den Größtfehler. Die Zusammenhänge sind in Bild 2 dargestellt.
Berechnung zufälliger Fehler
Beim Auftreten von zufälligen Fehlern ist es aufgrund ihres statistischen Charakters sinnvoll, eine Größe unter sonst gleichen Bedingungen mehrfach zu messen. Sind , , … die einzelnen Messwerte für eine Größe, so ergibt sich der Mittelwert x als arithmetisches Mittel:
Als Maß für die Streuung der Messwerte eignet sich der mittlere Fehler des arithmetischen Mittels, der folgendermaßen berechnet werden kann:
Eine Berechnung in dieser Weise ist nur sinnvoll, wenn die Anzahl n der Messungen einer Größe n 10 beträgt. Bei nur wenigen Messwerten kann man als mittleren Fehler ansetzen:
-
Arten von Fehlern
Hinweis:
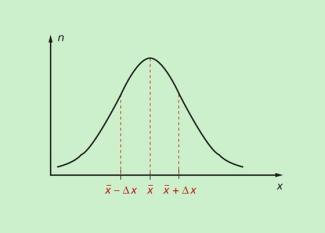
Bei Vorliegen einer sehr großen Anzahl von Messwerten ergibt sich für die Häufigkeitsverteilung der Messwerte eine Normalverteilung nach GAUSS (gaußsche Glockenkurve, s. Bild 3).
Es liegen dann 68,3 % der Messwerte im Bereich ± und 95,4 % im Bereich .
Abschätzung des Größtfehlers
Der Fehler beim Messen einer physikalischen Größe ergibt sich aus den zufälligen und den nicht erfassbaren systematischen Fehlern. Bei einer direkt messbaren Größe erhält man als Größtfehler:
Liegt für die Größe eine Messreihe vor, so wird als zufälliger Fehler der mittlere Fehler des arithmetischen Mittels eingesetzt.
Darstellung von Ergebnissen
Kennt man den Messwert x und Messfehler einer Größe, so kann man den Fehler als absoluten Fehler, als relativen Fehler oder als prozentualen Fehler angeben.
Der absolute Fehler ist ein Maß für die Abweichung der Messwerte vom wahren Wert.
Der relative Fehler / x verdeutlicht die Abweichung in Bezug auf den Messwert und ist Ausdruck für die Güte einer Messung.
Der prozentuale Fehler (/ x) % ist der in Prozent angegebene relative Fehler.
Die Zusammenhänge sind in der Übersicht unten auch am Beispiel verdeutlicht.
Die Angabe des Messergebnisses erfolgt in folgender Form:
Für das in der Übersicht unten dargestellte Beispiel würde das Ergebnis lauten: t = 7,6 s ± 0,2 s oder t = (7,6 ± 0,2) s
| Messwerte und Fehler | Beispiel |
| Messwert x | Zeit t = 7,6 s |
| absoluter Fehler | = ± 0,2 s |
| relativer Fehler / x | |
| prozentualer Fehler / x = (/ x )·100 % | / t = (± 0,026)·100 % = ± 2,6 % |
Allgemein gelten bei der Verknüpfung von Größen die nachfolgend genannten Zusammenhänge:
| Verknüpfung der Größen | Fehler | |
| Summe Differenz | z = x + y z = x - y | |
| Produkt Quotient | z = x · y | |
| Potenz | z = | |
Fehlerfortpflanzung
Wenn z. B. der elektrische Widerstand eines Bauelements bestimmt werden soll, kann man Stromstärke und Spannung messen und den Widerstand nach der Gleichung R = U/I berechnen. U und I sind fehlerbehaftet. Ähnlich ist das bei der Bestimmung der Geschwindigkeit durch Weg- und Zeitmessungen oder bei der Addition von fehlerbehafteten Geschwindigkeiten oder Kräften.
Die Fehler bei den einzelnen gemessenen Größen führen zu Fehlern bei den berechneten Größen. Wie sich die Fehler von gemessenen Größen auf den Fehler einer daraus berechneten Größe auswirken, zeigt die Übersicht oben.
Beispiel:
Die Geschwindigkeit wird durch Messung von Weg und Zeit ermittelt.
Dabei erhält man folgende Werte:
| s = 20 m | = ± 0,5 m |
| t = 1,6 s | = ± 0,2 s |
Damit erhält man als Geschwindigkeit:
v
v = 12,5 m/s = 45 km/h
Als Fehler ergibt sich bei einem Quotienten:
± 0,15 = 15 %
Mit v = 45 km/h ist dann:
= ± 6,75 km/h 7 km/h
Das Ergebnis lautet somit: Die Geschwindigkeit
beträgt
v = (45 ± 7) km/h.
Sie hat also einen Fehler von 15 %. Bei den Ergebnissen ist eine sinnvolle Rundung vorzunehmen. Fehler werden immer aufgerundet.
-
Normalverteilung nach GAUSS (gaußsche Glockenkurve)
Messfehler und grafische Darstellungen
Eine wichtige Aufgabe der Physik ist es, Zusammenhänge zwischen zwei Größen zu ermitteln, wobei diese beiden Größen gemessen werden und demzufolge fehlerbehaftet sind.
Als Beispiel betrachten wir eine Weg- und Zeitmessung bei einer Bewegung, die als gleichförmig angesehen werden kann. Ermittelt wurden die in der folgenden Tabelle dargestellten Messwerte.
| t in s | s in m |
| 0 | 30 |
| 2 | 40 |
| 4 | 60 |
| 6 | 68 |
| 8 | 76 |
| 10 | 97 |
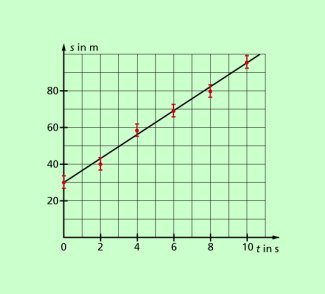
Bild 4 zeigt die entsprechende grafische Darstellung der Messwerte in einem s-t-Diagramm.
Dem physikalischen Sachverhalt nicht angemessen wäre es, die Punkte miteinander zu verbinden. Da alle Messwerte fehlerbehaftet sind, zeichnet man eine Ausgleichskurve.
Die Frage ist nun vor allem, ob man genauer bestimmen kann, wie diese Ausgleichskurve verläuft. Wir nehmen dazu an, dass der Fehler der Zeitmessung gegenüber dem Fehler der Wegmessung vernachlässigt werden kann.
-
Messwerte und Ausgleichskurve
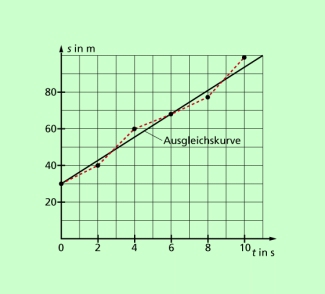
Eine erste Möglichkeit der genaueren Bestimmung des Verlaufs der Ausgleichskurve wäre, für jeden Messpunkt den Größtfehler des Weges in Form eines Fehlerbalkens zu markieren (Bild 5). Die Ausgleichskurve verläuft dann durch die Fehlerbalken hindurch. Im Beispiel haben wir für den Weg einen Fehler von = ± 2,5 m angenommen.
Die Funktionskurve der Ausgleichskurve lässt sich auch berechnen. Nehmen wir an, dass für sie die Gleichung
y = ax + b
gilt, dann kann man a bzw. b folgendermaßen berechnen:
Die Berechnung ergibt:
a = 6,5
b = 29,3
Die Gleichung für die Ausgleichsgerade lautet somit:
y = 6,5 · x + 29,3
Liegt ein nichtlinearer Sachverhalt vor und besteht eine Vermutung über die Art der Abhängigkeit, so kann man einen nichtlinearen Zusammenhang durch geschickte Wahl der Achsengrößen auf einen linearen Zusammenhang zurückführen.
Fehlerbetrachtung vor und nach Messungen
Fehlerbetrachtungen haben sowohl vor der Durchführung von Messungen als auch in Auswertung von Messungen ihre Bedeutung.
Besteht das Ziel der Messungen darin, eine physikalische Größe möglichst genau zu messen, so muss man vor der Messung u. a. folgende Fragen beantworten:
- Welches Messverfahren wähle ich?
- Wodurch können Messfehler verursacht werden?
- Gibt es Möglichkeiten, Fehler zu korrigieren, zu kompensieren oder zu minimieren?
- Welche Größen müssen besonders genau gemessen werden, weil ihr Fehler den Fehler des Gesamtergebnisses besonders stark beeinflusst?
- Ist es sinnvoll, eine Probemessung oder eine Kontrollmessung durchzuführen?
- Reicht eine einmalige Messung oder ist es zweckmäßig, die Messungen so oft zu wiederholen, dass eine statistische Auswertung (Fehlerrechnung) gemacht werden kann?
Beachte:
Die Genauigkeit von Messungen kann zumeist nur vor oder während der Messung beeinflusst werden. Deshalb sollte man Fehlerbetrachtungen schon vor Beginn der Messungen durchführen.
Nach der Durchführung der Messungen kann man in der Regel nur noch abschätzen, wie genau man gemessen hat, also folgende Fragen beantworten:
- Welche zufälligen und systematischen Fehler sind tatsächlich aufgetreten?
- Wie groß sind die einzelnen Fehler und die Größtfehler bei den einzelnen gemessenen Größen?
- Wie beeinflussen diese Fehler das Messergebnis? Wie groß ist der Fehler der zu bestimmenden Größe?
Beispiel: Die Fallbeschleunigung
Als Beispiel betrachten wir ein Experiment zur Bestimmung der Fallbeschleunigung g. Diese Naturkonstante kann man z. B. mithilfe eines Fadenpendels unter Nutzung der Gleichung
bestimmen, indem man für ein Fadenpendel der Länge l die Schwingungsdauer T misst und die Fallbeschleunigung mit der Gleichung
berechnet. Bei einer solchen Bestimmung der Fallbeschleunigung hängt der Messfehler von der Genauigkeit der Längenmessung und der Genauigkeit der Zeitmessung ab, wobei der Fehler der Zeitmessung mit dem Faktor 2 eingeht. Beträgt der absolute Fehler der Längenmessung des Pendels und der absolute Fehler der Messung der Schwingungsdauer , so ergibt sich als Fehler für die Fallbeschleunigung g:
Bei l = 70,0 cm mit = ± 1 cm und T = 1,64 s mit = ± 0,2 s erhält man:
± 0,26 oder 26 %
Eine andere Möglichkeit der Bestimmung der Fallbeschleunigung ist die über den freien Fall eines Körpers (Bild 1), die nachfolgend ausführlich dargestellt ist. Genutzt werden dabei die Gesetze des freien Falles.
Für den freien Fall gilt:
Damit kann der Wert für die Fallbeschleunigung experimentell bestimmt werden. Dazu wird die obige Gleichung nach der Fallbeschleunigung g umgestellt:
g
Weg und Zeit für den freien Fall eines Körpers müssen gemessen werden. Um einen möglichst genauen Wert für g zu erhalten, sollte die zu messende Fallzeit und damit der Fallweg nicht zu klein sein. Die Fallzeit wird mehrmals gemessen und anschließend ein Mittelwert berechnet. Die Auslösung des freien Falles erfolgt mit einem Magnetschalter, die Zeitmessung mit einer elektronischen Uhr (Bild 1).
Durchführung:
Der Fallweg beträgt s = 0,95 m.
| Messung Nr. | Zeit t in s |
1 | 0,47 0,42 0,48 0,44 0,45 0,42 0,44 0,43 0,46 0,45 |
Auswertung:
Aus der Messreihe für die Zeit kann folgender Mittelwert berechnet werden:
Für die Fallbeschleunigung errechnet man damit:
g g
Der experimentell ermittelte Wert stimmt relativ gut mit dem Tabellenwert (9,81 ) überein.
Der Messwert ist brauchbar, wenn der in diesem Falle bekannte genaue Wert im Fehlerintervall liegt.
Wir stellen nachfolgend die Überlegungen zur Messgenauigkeit und zum Fehlerintervall dar. Die Überlegungen sind ebenfalls in der Schrittfolge Vorbereitung - Durchführung - Auswertung dargestellt.
Vorbereitung:
Die Fallbeschleunigung wird nach g = 2 bestimmt, also sind Fallweg und Fallzeit zu messen.
Die Messung des Fallweges erfolgt mit einem Lineal mit cm-Teilung.
Zu beachten ist auch, dass die Entfernung von der Unterkante des Körpers bis zum Kontakt gemessen wird. Dabei können Parallaxefehler auftreten. Insgesamt dominieren bei der Wegmessung die zufälligen Fehler. Eine Mehrfachmessung mit Mittelwertbildung wäre sinnvoll.
Die Fallzeit muss besonders genau gemessen werden, da ihr Fehler mit dem Faktor 2 eingeht. Die Genauigkeit der Zeitmessung ist bei der Experimentieranordnung nicht beeinflussbar und im Wesentlichen durch die Genauigkeitsklasse des Messgerätes bestimmt. Da aber beim Fall zufällige Einflüsse (z. B. Luftbewegung) auftreten können, ist eine Messreihe mit anschließender Mittelwertbildung zweckmäßig.
Durchführung:
Es ist besonders darauf zu achten, dass sich während aller Messungen der Zeit der eingestellte Fallweg nicht verändert. Treten offensichtliche „Ausreißer“ auf, so kann man diese herausfallen lassen.
Auswertung:
Es können die Größtfehler bei der Messung von Fallweg und Fallzeit abgeschätzt und der Größtfehler der Fallbeschleunigung ermittelt werden.
Für den Fallweg ist der mögliche Ablesefehler entscheidend.
Bei einer cm-Teilung beträgt er:
± 0,5 cm
Nimmt man beim Lineal einen Gerätefehler von ± 1 % an, dann bedeutet das bei einer Messstrecke von ca. 1 m einen Fehler von:
± 1 cm
Der Größtfehler beträgt demzufolge:
= ± 1,5 cm
Für die elektronische Zeitmessung ist die Genauigkeitsklasse des Messgerätes entscheidend. Sie beträgt 1,0 bei einem Messbereich von 1 s, also beträgt der absolute Fehler 0,01 s. Nimmt man bei dem auf Hundertstel genau anzeigenden Zeitmesser noch einen zufälligen Fehler von 0,01 s an, dann ist:
= 0,02 s
Aus g = 2 erhält man nach den Regeln der Fehlerfortpflanzung für den absoluten Fehler der Erdbeschleunigung:
Mit den in der obigen Tabelle genannten Werten ergibt sich:
± 0,11
Der relative Fehler beträgt 11 %, der absolute Fehler ± 1,1 .
Als Ergebnis könnte man angeben:
g = (9,55 ± 1,1)
Anmerkung:
Bei den angegebenen Werten dominiert mit ca. 9 % der Fehler der Zeitmessung. Selbst bei Annahme eines Messfehlers bei der Zeitmessung von 0,01 s würde der relative Fehler von g immer noch 4,5 % oder ± 0,44 betragen. Auch dann würde der Tabellenwert im Fehlerintervall liegen.
-
Die Ausgleichskurve verläuft durch die Fehlerbalken hindurch