Interferenz am Gitter
Trifft Licht auf ein optisches Gitter, so wird es an den einzelnen Spalten gebeugt. Dieses von den einzelnen Spalten ausgehende Licht überlagert sich, es interferiert. Dabei treten Bereiche der Verstärkung und der Auslöschung auf.
Mithilfe von Interferenz am Gitter lässt sich die Wellenlänge von Licht experimentell bestimmen.
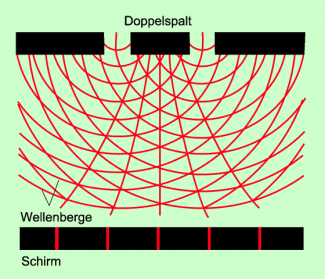
Trifft Licht auf ein optisches Gitter, so sind auf einem Bildschirm hinter dem Gitter typische Interferenzstreifen zu beobachten (Bild 1). Ein Gitter besteht aus sehr vielen eng beieinander liegenden Spalten.
Entstehen von Interferenzstreifen
Das auf das Gitter fallende Licht wird wie beim Doppelspalt (Bild 1) an jedem einzelnen Spalt gebeugt, d. h. es breitet sich nach dem betreffenden Spalt in den unterschiedlichsten Richtungen aus. Damit überlagert sich hinter dem Gitter das von den einzelnen Spalten ausgehende Licht. Es kommt in bestimmten Bereichen zur Verstärkung bzw. zur Auslöschung. Bringt man hinter dem Gitter einen Schirm an, so kann man auf ihm typische Interferenzstreifen, also helle und dunkle Linien, beobachten.
-
Interferenz von Licht durch Beugung
Die Breite der Interferenzstreifen ist von der Anzahl n der Spalte des Gitters abhängig. Es gilt:
Je größer die Anzahl der Spalte beim Gitter ist, desto geringer ist die Breite der Interferenzstreifen.
Wie beim Doppelspalt gilt auch für das Gitter:
- Bei Verwendung von einfarbigem Licht entstehen Interferenzstreifen in der Farbe dieses Lichtes.
- Bei Verwendung von weißem Licht erfolgt eine Aufspaltung in die einzelnen Farben. Es entsteht ein Spektrum, das aufgrund seiner Entstehung am Gitter auch als Gitterspektrum bezeichnet wird.
Gleichung für Interferenzmaxima
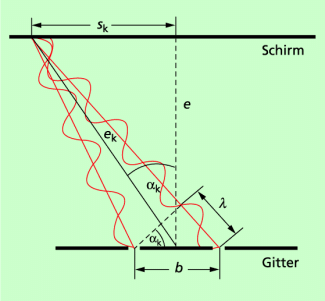
Die Lage der Interferenzmaxima kann man genauer ermitteln. Wir betrachten dazu einen Doppelspalt und die hellsten Interferenzstreifen nullter und erster Ordnung (Bild 3).
Wie bei mechanischen Wellen tritt eine Verstärkung dann auf, wenn bei gleicher Wellenlänge und fester Verschiebung zwischen zwei Wellenzügen sich jeweils Wellenberge und Wellentäler überlagern. Das ist dann der Fall, wenn die Verschiebung (Phasendifferenz) der Schwingungszustände zwischen zwei Wellenzügen
In Bild 3 ist das für eine Verschiebung von dargestellt. Für den Sinus des Winkels kann man unter Nutzung der Gitterkonstanten b für Interferenzmaxima allgemein schreiben:
Der Faktor k kann dabei die Werte 0, 1, 2, ... annehmen. Der Winkel lässt sich auch mithilfe von ausdrücken.
Dann erhält man:
Die Kombination der Gleichung (1) und (2) ergibt:
kann durch e ersetzt werden, da für kleine Winkel .
Dabei erhält man für die Interferenzmaxima am Gitter unter der Bedingung, dass die Entfernung des Schirms vom Gitter groß gegenüber dem Abstand der Interferenzstreifen ist, folgende Gleichung:
-
Lage der Interferenzmaxima am Gitter
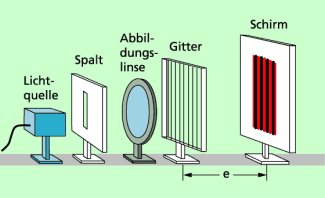
Bestimmen der Lichtwellenlänge
Die oben genannte Gleichung kann man nutzen, um die Wellenlänge von Licht zu bestimmen. Bild 4 zeigt eine mögliche Experimentieranordnung.
Die Gitterkonstante b, also der Abstand zweier Spalte voneinander, ist bei Gittern angegeben. Der Abstand zwischen Gitter und Schirm kann mit einem Lineal gemessen werden. Ebenso kann man auf dem Bildschirm den Abstand der Interferenzstreifen voneinander messen. Besonders geeignet sind wegen ihrer Helligkeit die Interferenzstreifen 1. Ordnung.
Beachte: In die Gleichung ist der Abstand zwischen den Interferenzmaxima 0. und 1. Ordnung einzusetzen. Das ist die Hälfte des Abstandes zwischen den beiden Maxima erster Ordnung.
Eine Gleichung für die Wellenlänge des Lichtes erhält man durch Umstellen der oben genannten Gleichung für die Interferenzmaxima:
-
Experimentieranordnung zur Bestimmung der Lichtwellenlänge
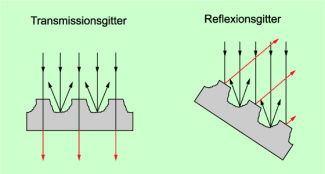
Optische Gitter
Ein Gitter wird hergestellt, indem man in eine Glasplatte oder in eine spiegelnde Metallplatte mit einem Diamanten in gleichen Abständen feine Furchen einritzt. Die nicht geritzten Teile wirken wie sehr schmale Spalte.
Nutzt man Glas, so geht das Licht durch die nicht geritzten Teile hindurch. Eine solche Art von Gitter bezeichnet man auch als Transmissionsgitter.
Bei einer spiegelnden Metallfläche geht dagegen dass Licht nicht hindurch, sondern wird an den nicht geritzten Stellen reflektiert. Eine solche Art von Gitter bezeichnet man deshalb als Reflexionsgitter.
Transmissionsgitter lassen sich auch relativ einfach auf fotografischem Wege herstellen: Zeichnet man auf ein Blatt Papier parallele schwarze Linien und fotografiert diese, so kann das Negativ als optisches Gitter verwendet werden.
Erfunden wurde das Gitter durch den deutschen Physiker JOSEPH VON FRAUNHOFER (1787-1826). FRAUNHOFER stellte mit einer speziell entwickelten Ritzmaschine Gitter mit einer Gitterkonstanten von bis zu her. Er nutzte dazu Glasplatten, in die feine Furchen eingeritzt wurden, und erhielt damit Transmissionsgitter.
Der amerikanische Physiker HENRY AUGUSTUS ROWLAND
(1848-1901) ritzte Spiegelmetall. Ihm gelang es, 20 000 Linien auf ein englisches Zoll zu ritzen. Das so entstandene Reflexionsgitter hatte eine Gitterkonstante von . Solche Reflexionsgitter werden nach ihrem Erfinder auch als ROWLAND-Gitter bezeichnet.
-
Transmissionsgitter und Reflexionsgitter