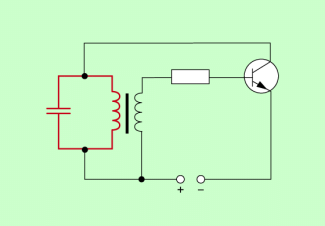
Meißnersche Rückkopplungsschaltung

Die elektromagnetischen Schwingungen in einem Schwingkreis klingen nach einmaliger Anregung relativ schnell wieder ab, weil elektromagnetische Energie durch den ohmschen Widerstand des Leitungsdrahtes in Wärme umgewandelt und dadurch dem Schwingkreis entzogen wird. Möchte man die Schwingung aufrecht erhalten, dann muss man dem Schwingkreis im Takt der Eigenschwingung und in der richtigen Phase Energie zuführen. Dies geschieht mithilfe einer meißnerschen Rückkopplungsschaltung.

Die meißnersche Rückkopplungsschaltung hat der deutsche Techniker ALEXANDER MEISSNER (1883-1958) im Jahre 1913 entwickelt. Während MEISSNER für seine Schaltung eine Elektronenröhre (Triode) nutzte, verwendet man heute anstelle von Röhren Transistoren. Die Basis des Transistors ist mit dem Schwingkreis gekoppelt. Fließt in der Spule des Schwingkreises ein Strom, so wird auch im Basisstromkreis des Transistors ein Strom induziert. Mit diesem Basisstrom fließt auch ein Kollektorstrom, der dem Schwingkreis Energie zuführt. Durch die Anordnung wird also erreicht, dass im Rhythmus der Schwingungen im Schwingkreis dem Schwingkreis selbst Energie zugeführt wird. Dies geschieht solange, bis die Verluste im Schwingkreis gerade durch die zugeführte Energie ausgeglichen werden. Die Schwingungsfrequenz ist dabei genau wie im einfachen Schwingkreis durch die thomsonsche Schwingungsgleichung festgelegt.
Mithilfe der meißnerschen Rückkopplungsschaltung kann man stabile sinusförmige elektromagnetische Schwingungen konstanter Amplitude und Frequenz erzeugen.