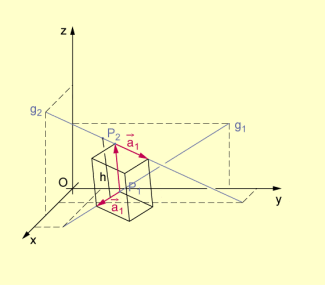
Anwendungen des Spatprodukts

Sind die drei Vektoren
$\overrightarrow{a}$ = $\left(\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right)$, $\overrightarrow{b}$ = $\left(\begin{array}{c}{b}_x\\ b_y\\ b_z\end{array}\right)$ und $\overrightarrow{c}$ = $\left(\begin{array}{c}{c}_x\\ c_y\\ c_z\end{array}\right)$
gegeben, so bezeichnet $(\overrightarrow{a}\times \overrightarrow{b})\cdot \overrightarrow{c}$ das Spatprodukt dieser drei Vektoren.

Das Spatprodukt lässt sich wie folgt berechnen:
$\left[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\right]=\left(\overrightarrow{a}\times \overrightarrow{b}\right)\cdot \overrightarrow{c}=\left|\begin{array}{ccc}{a}_x& b_x& c_x\\ a_y& b_y& c_y\\ a_z& b_z& c_z\end{array}\right|$

Außer dem Volumen eines Parallelepipeds kann mithilfe des Spatprodukts auch das Volumen eines Tetraeders ermittelt werden.

Ist OABC ein Tetraeder, das durch die drei Vektoren $\overrightarrow{a}=\overrightarrow{OA}$, $\overrightarrow{b}=\overrightarrow{OB}$ und $\overrightarrow{c}=\overrightarrow{OC}$ festgelegt ist, so bestimmen diese drei Vektoren auch ein Spat.

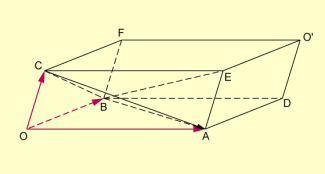
Zuerst zerlegt man dieses Spat in zwei volumengleiche Teile, indem es entlang der Ebene durch A, E, F, B zerteilt wird. Zeichnet man dann die Strecke $\overline{EB}$ ein, so „zerfällt“ der eine Teilkörper in drei Tetraeder OABC, ABCE und CBEF:

Die Tetraeder OABC und CBEF sind volumengleich, weil zum einen ihre Grundflächen OAB und CEF zueinander kongruent sind. Zum anderen stimmt die Höhe von C auf $\epsilon \left(OAB\right)$ mit der Höhe von B auf $\epsilon \left(CEF\right)$ überein, da die beiden betrachteten Ebenen parallel sind.

Die Tetraeder OABC und ABCE sind volumengleich, weil ihre Grundflächen OAC und ACE zueinander kongruent sind und in einer gemeinsamen Ebene liegen sowie B die gemeinsame Spitze über den entsprechenden Grundflächen ist.

Folglich gilt für das Volumen V(OABC) eines Tetraeders OABC:
$\text{V(OABC) =}\frac{\text{1}}{\text{6}}\left[\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}\right]=\frac{\text{1}}{\text{6}}\left[(\overrightarrow{OA}\times \overrightarrow{OB})\cdot \overrightarrow{OC}\right]$

Das Spatprodukt kann ferner zur Berechnung des Abstands eines Punktes von einer Ebene und zur Berechnung des Abstands zweier zueinander windschiefer Geraden benutzt werden.

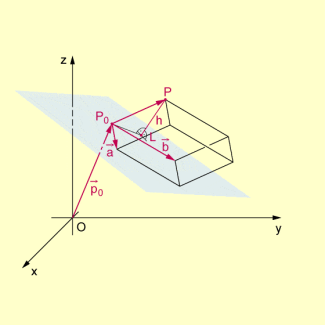
Sind eine Ebene $\epsilon$ durch ihre Gleichung $\overrightarrow{x}={\overrightarrow{p}}_0+r\overrightarrow{a}+s\overrightarrow{b}$ und ein Punkt P durch seine Koordinaten gegeben, so erhält man den (vorzeichenbehafteten) Abstand h des Punkts P von $\epsilon$ durch
$h=\frac{\left[\overrightarrow{a},\overrightarrow{b},\overrightarrow{P_{0}P}\right]}{\left|\overrightarrow{a}\times \overrightarrow{b}\right|}$.

Sind im Raum zwei zueinander windschiefe Geraden durch ihre Gleichungen $g_1\text{:}\overrightarrow{x}={\overrightarrow{p}}_1+t\overrightarrow{a}{}_1$ und $g_2\text{:}\overrightarrow{x}={\overrightarrow{p}}_2+t\overrightarrow{a}{}_2$ gegeben, so ist der Abstand h der beiden Geraden gleich dem Abstand der beiden zueinander parallelen Ebenen ${\epsilon }_1$ und ${\epsilon }_2$, die $g_1$ bzw. $g_2$ enthalten und eindeutig bestimmt sind.

Beide Ebenen sind dabei durch die Richtungsvektoren ${\overrightarrow{a}}_{1}und{\overrightarrow{a}}_2$ bestimmt. Der gesuchte Abstand ergibt sich dann z.B. als Abstand von $P_{2}von{\epsilon }_1$. Damit erhält man:
$\begin{array}{l}h=\frac{\left[{\overrightarrow{a}}_1,{\overrightarrow{a}}_2,\overrightarrow{P_1{P}_2}\right]}{\left|{\overrightarrow{a}}_1\times {\overrightarrow{a}}_2\right|}\end{array}$