Normalenvektoren einer Ebene im Raum
Unter dem Normalenvektor einer Ebene im Raum versteht man einen Vektor , der senkrecht zu ist.
In der folgenden Abbildung sind mehrere Normalenvektoren zu einer Ebene eingezeichnet. Alle diese Normalenvektoren haben dieselbe Richtung und sind damit parallel zueinander, unterscheiden sich jedoch im Richtungssinn und im Betrag.
-
Normalenvektoren einer Ebene im Raum
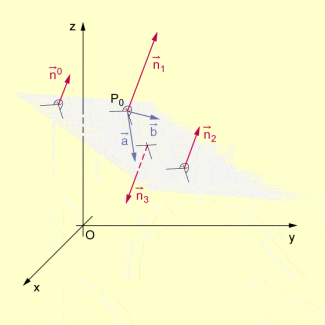
Aufgrund der eindeutig bestimmten Richtung eines Normalenvektors zu einer Ebene im Raum wird auch umgekehrt durch einen gegebenen Punkt und einen gegebenen Normalenvektor diejenige Ebene im Raum eindeutig bestimmt, die durch geht und senkrecht zu ist.
Für Abstandsprobleme wird oft ein Normaleneinheitsvektor verwendet, da dieser den Betrag 1 hat und sich damit zu Längenvergleichen anbietet. Ist ein beliebiger Normalenvektor einer Ebene im Raum, so erhält man den zugehörigen Normaleneinheitsvektor, indem man den Normalenvektor durch seinen Betrag dividiert:
Zu jeder Ebene im Raum gibt es genau zwei Normaleneinheitsvektoren, die sich nur im Richtungssinn unterscheiden.
- Ist eine Ebene im Raum durch ax + by + cz + d = 0 gegeben, so ist
ein Normalenvektor von .
Für eine Ebene im Raum gilt:
- Ist durch gegeben, so kann man mithilfe des Vektorprodukts einen Normalenvektor von berechnen:
Laut Definition des Vektorprodukts ist nämlich der das Vektorprodukt zweier Vektoren bildende Vektor senkrecht zu sowie senkrecht zu und damit auch senkrecht zu der durch aufgespannten Ebene.

