Schnittwinkel einer Geraden mit einer Ebene
Schneidet eine Gerade g die Ebene im Punkt S, so versteht man unter dem Schnittwinkel von g und den kleinsten Winkel, den eine beliebige Gerade aus , die durch S geht, mit g bildet.
Für die Berechnung von wird die Tatsache genutzt, dass der Komplementwinkel des Winkels zwischen einem Normalenvektor von und einem Richtungsvektor von g ist. Es gilt .
-
Schnittwinkel einer Geraden mit einer Ebene
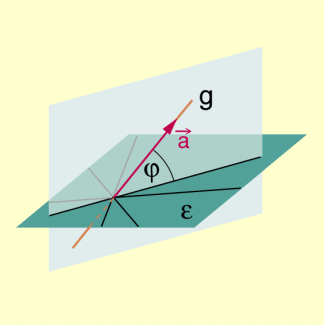
-
Winkel zwischen Gerade und Ebenennormale
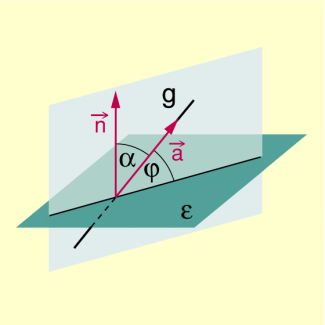
Durch diese Überlegung wird die Frage nach dem Schnittwinkel zwischen einer Geraden und einer Ebene auf das einfachere Problem des Schnittwinkels von zwei Geraden im Raum zurückgeführt.
Hat die Ebene die Gleichung , so ist ein Normalenvektor von . Ist die Gleichung von in der Koordinatenschreibweise, also , angegeben, dann gilt
.
Unter Verwendung der Definitionsgleichung des Skalarprodukts lässt sich nun als Formel für die Berechnung des Schnittwinkels zwischen und angeben:
Da ist, kann man auch schreiben:
Beispiel 1: Es ist der Schnittwinkel zwischen der Geraden
und der xy-Ebene zu ermitteln.
Da jeder Normalenvektor der xy-Ebene in z-Richtung weist, also z.B. die Gleichung
besitzt, gilt für den gesuchten Schnittwinkel
und damit .
Beispiel 2: Es ist der Schnittwinkel zwischen der Geraden
und der Ebene
zu ermitteln.
Mit
erhält man nach obiger Formel
und damit .

