Differenzialgleichungen zur Beschreibung von Federschwingungen

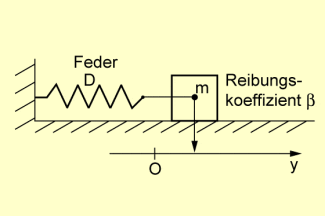
Auf den Körper wirken folgende Kräfte:

• die Trägheitskraft: $ma=my″\left(t\right)$ mit $m$ - Masse, $a$ - Beschl.
• die geschwindigkeitsproportionale Reibungskraft:
  $\beta v=\beta y\prime \left(t\right)$ mit $\beta$ - Reibungskoeffizient, $v$ - Geschwindigkeit
• die rücktreibende Federkraft (hookesches Gesetz):
  $Dy\left(t\right)$ mit $D$ - Federkonstante, $y$ - Auslenkung

Die Summe der betrachteten Kräfte ist gleich der von außen wirkenden Kraft, hier also 0. Es gilt demzufolge:
$my″\left(t\right)+\beta y\prime \left(t\right)+Dy\left(t\right)=0$

Dividiert man diese Differenzialgleichung 2. Ordnung durch m, so ergibt sich
$y″\left(t\right)+\frac{\beta }{m}y\prime \left(t\right)+\frac{D}{m}y\left(t\right)=0(\ast )$.

Diese Gleichung entspricht mit den Zuordnungen $q=\frac{\beta }{m}undr=\frac{D}{m}$ der Gleichung $f″\left(x\right)+qf\prime \left(x\right)+rf\left(x\right)=0$.

Gleichung $(\ast )$ wird mit dem Lösungsansatz $y\left(t\right)=e^{k\text{‌}t}$ gelöst.

Es gilt $y\prime \left(t\right)=k{e}^{k\text{‌}t}undy″\left(t\right)=k^2{e}^{k\text{‌}t}$.

Durch Einsetzen in die Differenzialgleichung $(\ast )$ erhält man
$k^2{e}^{kt}+\frac{\beta }{m}k{e}^{kt}+\frac{D}{m}{e}^{kt}=e^{kt}\left(k^2+\frac{\beta }{m}k+\frac{D}{m}\right)=0$
und daraus nach Division durch $e^{kt}$ die charakteristische Gleichung
$k^2+\frac{\beta }{m}k+\frac{D}{m}=0$
mit den Lösungen
$k_{1/2}=-\frac{\beta }{2m}\pm \sqrt{{\left(\frac{\beta }{2m}\right)}^2-\frac{D}{m}}.$

Ist der Reibungskoeffizient $\beta$ zwar nicht vernachlässigbar, aber dennoch hinreichend klein, so überwiegt im Radikand der Wurzel der Anteil $\frac{D}{m}$, der Radikand wird negativ.

Wegen $q=\frac{\beta }{m}$ (s. o.) ergibt sich als allgemeine Lösung
$y\left(t\right)=e^{-\frac{\beta }{2m}t}\left(c_1\cos \omega t+c_2\sin \omega t\right)mit{c}_1,c_2\in ℝund\omega =\sqrt{\frac{D}{m}-{\left(\frac{\beta }{2m}\right)}^2}$.

Da $\frac{\beta }{2m}$ als Dämpfungskonstante $\delta$ bezeichnet wird, heißt die Lösung schließlich $y\left(t\right)=e^{-\delta t}\left(c_1\cos \omega t+c_2\sin \omega t\right)mit{c}_1,c_2\in ℝ$.

Diese Gleichung besagt, dass die Federanordnung in eine gedämpfte Schwingung gebracht werden kann.

Beispiel: Es soll nun eine Federanordnung mit $m=1kg,D=\mathrm{1,04}kg\cdot s^{-2}und\beta =\mathrm{0,4}kg\cdot s^{-1}$ betrachtet werden.

Hier gilt    $\begin{array}{l}\frac{D}{m}=\mathrm{1,04}\cdot s^{-2}>>{\left(\frac{\beta }{2m}\right)}^2={\left(\mathrm{0,2}{s}^{-1}\right)}^2=\mathrm{0,04}{s}^{-2}\\ \delta =\frac{\beta }{2m}=\mathrm{0,2}{s}^{-1}\\ \omega =\sqrt{\mathrm{1,04}{s}^{-2}-\mathrm{0,04}{s}^{-2}}=1s^{-1}.\end{array}$

Die Schwingungsgleichung für diese Federanordnung lautet:
$y\left(t\right)=e^{-\mathrm{0,2}{s}^{-2}\cdot t}\left(c_1\cos \left(1s^{-1}\cdot t\right)+c_2\sin \left(1s^{-1}\cdot t\right)\right)$

Wird die Masse aus der Ruhelage heraus $\left(y\left(0\right)=0\right)$ mit einer Geschwindigkeit von $10m{s}^{-1}$ in die positive y-Richtung weggestoßen $\left(y\prime \left(0\right)=10m{s}^{-1}\right),$ so lassen sich die Parameter $c_{1}und{c}_2$ der allgemeinen Lösung bestimmen:

$y\left(0\right)=0$ in die allgemeine Lösung einsetzen:
$y\left(0\right)=0=e^{-\delta \cdot 0}\left(c_1\cos (\omega \cdot 0)+c_2\sin (\omega \cdot 0)\right)=1\cdot \left(c_1\cdot 1+c_2\cdot 0\right)=c_1=0.$

Erste Ableitung der Lösung:
$\begin{array}{l} y\prime \left(t\right)=\left[e^{-\delta t}\left(c_1\cos \omega t+c_2\sin \omega t\right)\right]\prime \\ \text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}\text{‌}=-\delta e^{-\delta t}\left(c_1\cos \omega t+c_2\sin \omega t\right)+e^{-\delta t}\left(-c_1\omega \sin \omega t+c_2\omega \cos \omega t\right)\\ y\prime \left(0\right)=10m{s}^{-1}=-\delta e^{-\delta \cdot 0}\left(c_1\cos (\omega \cdot 0)+c_2\sin (\omega \cdot 0)\right)\\ +e^{-\delta \cdot 0}\left(-c_1\omega \sin (\omega \cdot 0)+c_2\omega \cos (\omega \cdot 0)\right)\\ =-\delta \left(c_1+0\right)+\omega \left(0+c_2\right)\\ y\prime \left(0\right)=10m{s}^{-1}=-\delta \cdot c_1+\omega c_2.\\ Da{c}_1=0ist,gilt\omega c_2=10m{s}^{-1}bzw.c_2=\frac{10m{s}^{-1}}{\omega }=\frac{10m{s}^{-1}}{1s^{-1}}=10m.\end{array}$

Die Lösung des Anfangswertproblems lautet:
$y\left(t\right)=10m\cdot e^{-\mathrm{0,2}s{}^{-1}\cdot t}\cdot \sin \left(1s^{-1}\cdot t\right)$

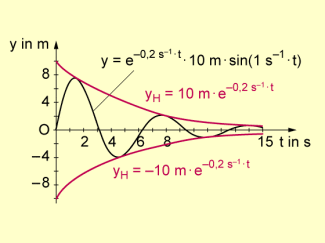
Nachdem eine gedämpfte Schwingung untersucht wurde, soll nun für die gleiche Federanordnung geklärt werden,

1. welche Schwingung ausgeführt wird, wenn keine Reibung vorhanden wäre und
2. wie groß der Reibungskoeffizient bzw. die Dämpfungskonstante sein müsste, damit die Anordnung überhaupt nicht schwingen kann.

Im ersten Fall gilt $\beta =0$ und damit auch $\delta =0$ Aus diesen Werten errechnet sich die Kreisfrequenz $\omega =\mathrm{1,020}{s}^{-1}$ und damit ergibt sich für die allgemeine Lösung der Schwingungsgleichung
$y\left(t\right)=e^{-0\cdot t}\left(c_1\cos \omega t+c_2\sin \omega t\right)=c_1\cos \mathrm{1,020}{s}^{-1}\cdot t+c_2\sin \mathrm{1,020}{s}^{-1}\cdot t.$

Unter den bereits betrachteten Anfangsbedingungen ergibt sich die ungedämpfte Schwingung $y\left(t\right)=\mathrm{9,806}m\cdot \sin \mathrm{1,020}{s}^{-1}\cdot t$ (siehe Graph 1 in der folgenden Abbildung).

Die Frequenz der Schwingung ist hier etwas höher als bei der gedämpften Schwingung (siehe Graph 2 in der folgenden Abbildung).

Die Federanordnung kann nicht mehr schwingen, wenn die Reibung und damit der Wert für $\beta$ mindestens so groß geworden ist, dass die charakteristische Gleichung $k^2+\frac{\beta }{m}k+\frac{D}{m}=0$ eine reelle Doppellösung besitzt.

In diesem Falle gilt $\frac{D}{m}={\left(\frac{\beta }{2m}\right)}^{2}oder\beta =2\sqrt{D\cdot m}$.

Für die betrachtete Federanordnung liegt dieser Grenzwert bei $\beta =\mathrm{2,040}kg{s}^{-1}bzw.bei\delta =\mathrm{1,020}{s}^{-1}$.

Als allgemeine Lösung erhält man dann $y\left(t\right)=c_1{e}^{-\mathrm{1,020}{s}^{-1}\cdot t}+c_{2}t\cdot e^{-\mathrm{1,020}{s}^{-1}\cdot t}$.

Werden auch hier die bekannten Anfangsbedingungen benutzt, so erhält man $y\left(t\right)=10m\cdot t\cdot e^{-\mathrm{1,020}{s}^{-1}\cdot t}$ (siehe Graph 3 in der folgenden Abbildung).