Lineare Differenzialgleichungen 1. Ordnung
Die einfache lineare Differenzialgleichung 1. Ordnung lässt sich nicht durch Trennen der Variablen lösen. Wird die Differenzialgleichung nämlich in die Form gebracht, so erkennt man, dass sich die rechte Seite nicht als Produkt schreiben lässt, was Voraussetzung für das Trennen der Variablen ist.
Die Lösung der inhomogenen Gleichung kann jedoch ausgehend von der Lösung der entsprechenden homogenen Gleichung gefunden werden.
Beispiel 1:
Allgemeine Lösung der Differenzialgleichung
(1.) Lösung der homogenen Gleichung
Diese Gleichung entspricht der Differenzialgleichung mit (siehe Beispiel 2).
Die Gleichung besitzt demzufolge die Lösung .
(2.) Partikuläre Lösung der inhomogenen Gleichung
Es gilt, eine geeignete Funktion als Lösungsansatz zu finden, die dann einer Probe unterworfen wird. Generell sollte die Suche mit dem Funktionstyp begonnen werden, der in der Inhomogenität vorliegt. Hier empfiehlt sich ein Ansatz mit der linearen Funktion .
Ansatz:
Probe in der Differenzialgleichung:
Die Gleichung wird nur für zu einer wahren Aussage.
Eine partikuläre Lösung der inhomogenen Gleichung ist demnach:
(3.) Allgemeine Lösung der inhomogenen Gleichung
Da die allgemeine Lösung einer inhomogenen linearen Differenzialgleichung gleich der Summe aus einer partikulären Lösung dieser inhomogenen und der allgemeinen Lösung der zugehörigen homogenen linearen Differenzialgleichung ist, gilt:
hier also
-
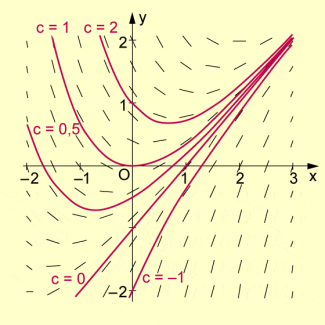
Lösungen der linearen Differenzialgleichung f′(x)+f(x)−x=0
Nach dem im Beispiel gezeigten Vorgehen lassen sich eine Reihe anderer linearer Differenzialgleichungen 1. Ordnung lösen. Es gibt sogar eine allgemeine Lösungsformel für die Differenzialgleichung , die hier aber nicht behandelt werden soll. Wir beschränken uns vielmehr auf den Fall konstanter Koeffizienten, für die sich in Analogie zu den Differenzengleichungen eine allgemeine Lösung entwickeln lässt. Der Lösungsweg folgt dem vorhergehenden Beispiel.
Beispiel 2:
Lösung einer linearen Differenzialgleichung 1. Ordnung mit konstanten Koeffizienten
Es soll die Lösung einer Differenzialgleichung der Form
ermittelt werden.
Für q = 0 vereinfacht sich die Differenzialgleichung zur einfachen Integrationsaufgabe mit . als Lösung. Deshalb soll nachfolgend gelten.
(1.) Die allgemeine Lösung der homogenen linearen Differenzialgleichung erhält man durch Trennen der Variablen:
Lässt man zu, so kann sich das Vorzeichen von y in c widerspiegeln und als allgemeine Lösung ergibt sich:
(2.) Partikuläre Lösung der inhomogenen Differenzialgleichung :
Als Lösungsansatz wird eine konstanten Funktion verwendet:
Ansatz:
Probe:
Um diese Gleichung zu einer wahren Aussage zu machen, muss gelten. Eine partikuläre Lösung der inhomogenen Gleichung ist demnach .
(3.) Allgemeine Lösung der inhomogenen Gleichung
Wegen gilt im vorliegenden Fall:
Das Ergebnis des letzten Beispiels lässt sich als Satz zusammenfassen:
Die allgemeine Lösung einer Differenzialgleichung 1. Ordnung mit konstanten Koeffizienten ist die Funktion
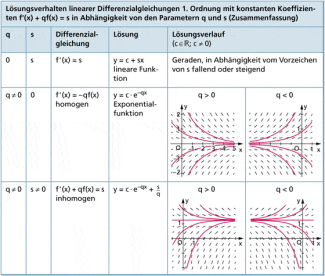
In der folgenden Abbildung wird das Lösungsverhalten linearer Differenzialgleichungen 1. Ordnung mit konstanten Koeffizienten in Abhängigkeit von den Parametern q und s systematisierend dargestellt.
-
Lösungsverhalten linearer Differenzialgleichungen 1. Ordnung in Abhängigkeit von q und s