Leonhard Euler
* 15. März 1707 Basel
† 18. September 1783 St. Petersburg
LEONHARD EULER war einer der produktivsten Wissenschaftler, was sowohl Fülle und Bedeutsamkeit als auch Vielseitigkeit seiner Beiträge angeht. Zwar gilt er vor allem als Mathematiker, doch hat er unter Nutzung der Mathematik, insbesondere der analytischen Methode, auch andere wissenschaftliche Gebiete (Mechanik, Planetenbewegung, Strömungslehre, Optik u.a.) erfolgreich bearbeitet.
Seine mathematischen Arbeiten beschäftigten sich vor allem mit Problemen der Analysis und der Zahlentheorie.
Aus dem Leben von EULER
LEONHARD EULER wurde am 15. April 1707 als Sohn eines Pfarrers in Basel geboren. Sein mathematisch interessierter Vater hatte bei JAKOB BERNOULLI Vorlesungen gehört und unterrichtete den Knaben zunächst selbst. Die Jugend verbrachte EULER in dem Ort Liehen bei Basel und besuchte dort die Schule. Nachdem sich seine mathematische Begabung gezeigt hatte, bezog er im Jahre 1720 (also mit 13 Jahren) die Universität von Basel, wo er seine Ausbildung u.a. durch JOHANN BERNOLLI – zusammen mit dessen Söhnen Niklaus und Daniel – erfuhr.
Bereits 1724 wurde LEONHARD EULER zum philosophischen Magister ernannt. 1727 ging er nach St. Petersburg. Er folgte einer Einladung von NIKLAUS und DANIEL BERNOULLI, mit denen er seit der Baseler Zeit befreundet war und die bereits an der Petersburger Universität wirkten. 1730 wurde EULER Professor für Physik und 1733 auch für Mathematik.
Die Jahre in Petersburg waren ausgefüllt mit rastloser Arbeit und fruchtbar für EULERS wissenschaftliches Schaffen. Unter anderem nahm er an der kartografischen Erfassung des damals noch wenig erforschten Russland teil. Überanstrengung bei dieser Arbeit, verbunden mit einer Infektion, führten zu einer fast völligen Erblindung seines rechten Auges (1738).
Nicht zuletzt weil sich die politischen Verhältnisse in Russland verschlechtert hatten, nahm EULER eine Einladung des preußischen Königs FRIEDRICH II. nach Berlin an, wo er Direktor der mathematischen Klasse der Akademie wurde. In den mehr als zwei Jahrzehnten seines Berliner Aufenthaltes – er wohnte lange Zeit in der Bärenstraße (der heutigen Behrenstraße) im Haus Nr. 21 – entstanden einige seiner bedeutendsten Werke.
Doch das anfänglich gute Verhältnis zum König trübte sich immer mehr. Dieser war über EULER enttäuscht, der das Hofleben mied, kein glänzender Unterhalter war wie die französischen Mathematiker und dessen mathematische Forschungen ihn wenig interessierten. Bald spottete der König über seinen „einäugigen Geometer“ und zog andere ihm vor.
Gekränkt und verbittert kehrte EULER 1766 nach Petersburg zurück, wo ihn die Zarin KATHARINA II. ehrenvoll empfing und ihm ausgezeichnete Arbeitsbedingungen sicherte. Damit konnte er ohne materielle Sorgen leben. EULER hatte 1734 geheiratet, aus der Ehe waren 13 Kinder (von denen fünf am Leben blieben) und 38 Enkelkinder hervorgegangen. Ein Zeitgenosse berichtete über ihn:
Ein Kind auf den Knien, eine Katze auf dem Rücken, so schrieb er seine unsterblichen Werke.
Mit zunehmendem Alter ließ die Sehkraft auch des zweiten Auges nach, sodass EULER nahezu blind war. Dennoch entstand danach noch etwa die Hälfte seiner wissenschaftlichen Arbeiten. Mit eiserner Energie und einem phänomenalen Gedächtnis führte er selbst schwierige Operationen im Kopf aus. In diesen Jahren entstand seine „Vollständige Anleitung zur Algebra“ als Muster eines vorbildlichen Lehrbuches, das über lange Zeit das Standardwerk für die mathematische Ausbildung wurde. Er diktierte es einem ehemaligen Schneidergesellen und prüfte an dessen Verständnis, ob er den Stoff klar dargestellt hatte.
Am 18. September 1783 wurde EULER von einem Schlaganfall getroffen und verstarb noch am gleichen Tage. Er wurde zunächst auf dem Smolenski-Friedhof beigesetzt und später auf den Friedhof des Alexander-Newski-Klosters umgebettet nahe der Grabstelle LOMONOSSOWS. In Liehen, dem Ort seiner Kindheit, erinnert eine Bronzetafel an EULER mit der Inschrift Er war ein großer Gelehrter und ein gütiger Mensch.
Zu EULERS mathematischen Leistungen
Ohne Zweifel war LEONHARD EULER einer der produktivsten Wissenschaftler, sowohl was die Fülle und Bedeutsamkeit als auch was die Vielseitigkeit seiner Beiträge angeht. Zwar gilt er vor allem als Mathematiker, doch hat er auch andere Gebiete – oft unter Nutzung der Mathematik – bereichert. Einige seiner Veröffentlichungen seien hier exemplarisch aufgezählt:
| 1731 (erschienen 1739) | Werk über Musiktheorie |
| 1736 | Buch über Mechanik |
| 1744 | Himmelsmechanik |
| 1746 | Neue Theorie des Lichts und der Farben (darin Zusammenhang zwischen Farbe und Wellenlänge) |
| 1749 | Buch über Schiffsbau Übersetzung und Bearbeitung des englischen Werkes „Neue Grundsätze der Artillerie“ (New Principles of Gunnery) von BENJAMIN ROBIN; nach diesem Buch wurde NAPOLEON zum Artillerieoffizier ausgebildet |
| 1751 | erste Mondtheorie |
| 1753 | Buch über Hydromechanik und Turbinenbau |
| 1758 | Auffinden der Kreiselgleichung |
| 1760 | geographischer Atlas |
| 1768 | Briefe an die deutsche Prinzessin (über Physik und Philosophie) |
Die Würdigung der mathematischen Beiträge EULERS muss sich auf einige ausgewählte Beispiele beschränken.
EULERS besondere Liebe galt der Zahlentheorie. „Er rechnete, wie andere atmen“, sagte ein Zeitgenosse über ihn. Es wird glaubhaft berichtet, dass EULER in einer Zeit, da er nachts keinen Schlaf fand, die Potenzen der natürlichen Zahlen bis 20 im Kopf bis zu berechnete und die Ergebnisse dauerhaft behielt.
Bei der Suche nach Termen, die nur Primzahlen liefern, hatte PIERRE DE FERMAT im Jahre 1640 den Term gefunden, der für die Zahlen 1, 2, 3 und 4 tatsächlich auf Primzahlen führt. Für n = 5 erhält man die Zahl , die man auch für eine Primzahl hielt.
EULER fand heraus, dass sich diese Zahl als Produkt schreiben lässt, wobei er sich wahrscheinlich einiger von ihm gefundener Hilfssätze bediente. Er selbst nannte in diesem Zusammenhang den Term , bei dem für die natürlichen Zahlen bis 39 tatsächlich jeweils Primzahlen herauskommen.
Andere Theoreme FERMATS konnte EULER dagegen beweisen, z.B. den folgenden Satz:
- Jede Primzahl der Form 4n + 1 lässt sich als Summe zweier einander teilerfremder Quadrate schreiben
(etwa ).
Er bewies auch den sogenannten „Kleinen FERMAT“ (kleinen fermatschen Satz):
- Für alle Primzahlen p und alle natürlichen Zahlen a ist stets durch p teilbar
(für p = 3 und a = 2 bzw. a = 5 gilt z.B. und ).
Ganz andersartig ist das Problem, mit dessen Lösung er sogar eine neue mathematische Teildisziplin, die Topologie begründete.
Ausgangspunkt dafür war das „Königsberger Brückenproblem“. In dieser Stadt gab es eine Insel, die von zwei Flussarmen umgeben ist, über die sieben Brücken führen. Niemand hatte einen Weg gefunden, bei dem man jede dieser Brücken genau einmal überschreitet. EULER wies nach, dass das auch nicht möglich ist, wenn es mehr als zwei Gebiete gibt, für die die Anzahl der Zugangsbrücken ungerade ist.
-
Königsberger Brückenproblem
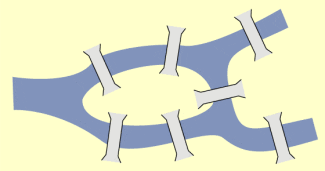
Aus gleichen Überlegungen ergibt sich, dass man eine Figur nicht in einem Zuge zeichnen kann, wenn es in ihr mehr als zwei Knotenpunkte gibt, bei denen eine ungerade Zahl von Linien hin- bzw. wegführt.
-
Topologisches Problem
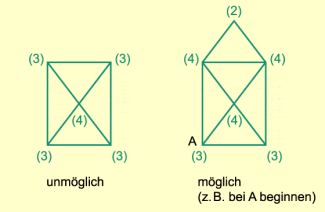
Mit ähnlichen Überlegungen bewies LEONHARD EULER den nach ihm benannten Polyedersatz:
- Für alle konvexen Polyeder gilt:
(wobei e die Anzahl der Ecken, f die der Flächen und k die der Kanten bedeutet)
Seinen Namen trägt auch die eulersche Gerade. Für alle Dreiecke gilt, dass der Schnittpunkt der Höhen, der Schnittpunkt der Mittelsenkrechten und der der Seitenhalbierenden auf einer (nämlich dieser) Geraden liegen.
1744 erschien EULERS Lehrbuch über Variationsrechnung, das sich mit Problemen der Berechnung von Extremwerten (Maxima und Minima) befasste.
1748 veröffentlichte er die erste analytische Geometrie der Kegelschnitte in Lehrbuchform, worin sich auch Entwicklungen von Reihen für und finden.
LEONHARD EULER hat mehr als 900 wissenschaftliche Abhandlungen verfasst, mehr als die Hälfte davon während seiner Blindheit. Dank des großen Ansehens, das er genoss, haben viele Begriffe und Symbole, die er in seinen Werken einführte oder übernahm, durch ihn Eingang in die Mathematik gefunden und werden heute noch benutzt. Dazu gehören beispielsweise:
- die Bezeichnungen a, b, c für die Seiten bzw. für die Winkel eines Dreiecks;
- das Zeichen für die Kreiszahl;
- sin, cos und tan als Streckenverhältnisse;
- die Zahl e (auch eulersche Zahl genannt) als Grenzwert von und als Basis der natürlichen Logarithmen;
- das Zeichen für den Differenzenquotienten;
- das Summenzeichen ;
- das Symbol i für ;
- das Symbol für Funktionen (für die er auch eine Definition angab)
CARL FRIEDRICH GAUSS (1777 bis 1855) schrieb über EULER:
Von keinem anderen Mathematiker neuerer oder älterer Zeit kann man eine solche fast unbegreifliche Schnelligkeit in den schwierigsten Arbeiten bei einer solchen unerschöpflichen Fruchtbarkeit an neuen Ideen und Hilfsmitteln rühmen. Alle Teile der Mathematik bearbeitete er, und die meisten erhielten unter seinen Händen eine ganz neue Gestalt.
Suche nach passenden Schlagwörtern
- platonische Körper
- Seitenhalbierende
- Exponentialfunktionen
- Minimum
- Differenzenquotient
- Mittelsenkrechten
- reguläre Polyeder
- Potenzen
- Kegelschnitte
- Kreiszahl
- Maximum
- Extrema
- Königsberger Brückenproblem
- eulersche Gerade
- Primzahlen
- Bernoulli
- Himmelsmechanik
- fermatscher Satz
- Funktionen
- Reihen
- Höhen
- Extremwerte
- analytische Geometrie
- Summenzeichen

