Numerische Lösungsverfahren für Differentialgleichungen

Die Grundidee der meisten numerischen Lösungsverfahren für Differenzialgleichungen 1. Ordnung besteht im Polygonzugverfahren. Mathematisch beruht es auf dem Übergang von der Differenzialgleichung zu einer entsprechenden Differenzengleichung.

In einer Differenzialgleichung 1. Ordnung in expliziter Form $f\prime \left(x\right)=G\left(x;\text{ f}\left(\text{x}\right)\right)$ kann man den Differenzialquotienten
$f\prime \left(x\right)=\underset{h\to 0}{\lim }\frac{f\left(x+h\right)-f\left(x\right)}{h}$
bei hinreichend klein festgelegtem h näherungsweise durch den Differenzenquotienten
$\frac{f\left(x+h\right)-f\left(x\right)}{h}$
ersetzen.

Unter dieser Voraussetzung gilt für $f\prime \left(x\right)=G\left(x;f\left(x\right)\right)$ (1)

$G\left(x;f\left(x\right)\right)=f\prime \left(x\right)\approx \frac{f\left(x+h\right)-f\left(x\right)}{h}$ bzw. $h\cdot G\left(x;f\left(x\right)\right)=h\cdot f\prime \left(x\right)\approx f\left(x+h\right)-f\left(x\right)=\Delta f\left(x\right)$ oder kürzer: $h\cdot G\left(x;f\left(x\right)\right)\approx \Delta f\left(x\right)$ (2)

Setzt man hier statt des „ungefähr gleich“ ein „ist gleich“, so erhält man eine Gleichung für eine Funktion $\overline{f}$, die eine Näherung für f ist. Es gilt
$h\cdot G\left(x;\overline{f}\left(x\right)\right)=\Delta \overline{f}\left(x\right)\text{ bzw}\text{. }\overline{f}\left(x+h\right)=\overline{f}\left(x\right)+hG\left(x;\overline{f}\left(x\right)\right)$
oder
$\Delta \overline{f}\left(x\right)=L\left(x;\overline{f}\left(x\right)\right)\text{ mit }L\left(x;\overline{f}\left(x\right)\right)=h\text{ G}\left(x;\overline{f}\left(x\right)\right)$ (3).

Gleichung (3) ist eine Differenzengleichung. Sie kann numerisch gelöst werden. Falls es sogar eine lineare Differenzengleichung ist, lässt sie sich exakt lösen. Die jeweils erhaltene Funktion $\overline{y}=\overline{f}\left(x\right)$ ist eine Näherungslösung der Differenzialgleichung (1).

Beispiel 1: Die Differenzialgleichung
$f\prime \left(x\right)=r\left(\frac{1-f\left(x\right)}{G}\right)f\left(x\right)$
mit $r=\mathrm{0,5}$ und $G=100$ soll in eine Differenzengleichung mit $h=2$ umgewandelt und eine Näherungslösung der Differenzialgleichung für die Anfangsbedingung $f\left(0\right)=4$ angegeben werden.

Aus $\mathrm{0,5}=\left(1-\frac{f\left(x\right)}{100}\right)f\left(x\right)=f\prime \left(x\right)=\underset{h\to 0}{\lim }\frac{f\left(x+h\right)-f\left(x\right)}{h}\approx \frac{f\left(x+2\right)-f\left(x\right)}{2}$erhält man $f\left(x+2\right)-f\left(x\right)=\Delta f\left(x\right)\approx \mathrm{0,5}\cdot 2\left(1-\frac{f\left(x\right)}{100}\right)f\left(x\right)bzw.\left(1-\frac{\overline{f}\left(x\right)}{100}\right)\overline{f}\left(x\right)$.

Mit den Transformationen $\overline{f}\left(x\right)=y_{i}und\Delta \overline{f}(x)=y_{i+1}-y_i$ entsteht die Differenzengleichung in der Form $y_{i+1}=2y_i-\mathrm{0,01}{y}_i{}^2$.

Man erhält dafür folgende Wertetabelle:

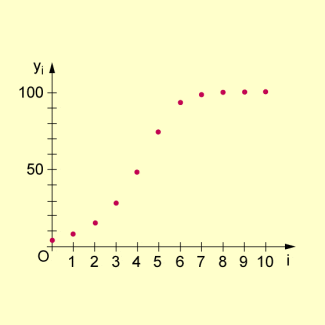
Die in der Tabelle berechneten Werte bilden eine Näherungslösung für das hier gestellte Anfangswertproblem. Diese Näherungslösung ist in der folgenden Abbildung grafisch dargestellt.

Die Tatsache, dass eine Lösung der Differenzengleichung (3) eine Näherungslösung der Differenzialgleichung (1) ist, soll am Beispiel der linearen Differenzen- und Differenzialgleichungen belegt werden.

Beispiel 2:: Die Differenzialgleichung $f\prime \left(x\right)+qf\left(x\right)=s\text{ mit x}\text{, q}\text{, s}\in ℝ\text{ und q}\ne \text{0}$ besitzt folgende Lösung:
$y=f\left(x\right)=c\cdot e^{-qx}+\frac{s}{q}\text{ mit }c\in ℝbel$. (4)

Dieselbe Differenzialgleichung kann nach obigem Vorgehen auch in die Differenzengleichung
$\Delta \overline{f}\left(x\right)+hq\overline{f}\left(x\right)=hs\text{ mit }h\ne 0$ (5)
umgewandelt werden.

Unter Nutzung der Transformationen $\overline{f}\left(x\right)=y_i\text{ und }\Delta \overline{f}(x)=y_{i+1}-y_i$ erhält man daraus $y_{i+l}-y_i+hq{y}_i=hs\text{ bzw}{\text{. y}}_{\text{i}\text{+l}}=\left(1-hq\right)y_i+hs$.

Diese Differenzengleichung besitzt die Lösung $y_i=c{\left(1-hq\right)}^i-\frac{hs}{1-hq-1}=c{\left(1-hq\right)}^i+\frac{s}{q}$ bzw. $\left(wegen\text{ i}=\frac{x-x_0}{h}\right)$
$\overline{f}\left(x\right)=c{\left(1-hq\right)}^{\frac{x-x_0}{h}}+\frac{s}{q}=c{\left(1-hq\right)}^{\frac{x}{h}}\cdot {\left(1-hq\right)}^{-\frac{x_0}{h}}+\frac{s}{h}$.

Mit $c\prime =c\cdot {\left(1-hq\right)}^{-\frac{x_0}{h}}$ ergibt sich als Lösung von (5):
$\overline{f}\left(x\right)=c\prime {\left(1-hq\right)}^{\frac{x}{h}}+\frac{s}{q}$ (6)

Ist neben der Differenzialgleichung $f\prime \left(x\right)+qf\left(x\right)=s$ auch die Anfangsbedingung $f\left(0\right)=y_0$ gegeben, so müssen in den Gleichungen (4) und (6) die Parameter bestimmt werden.

Bestimmung für Gleichung (4):
$\begin{array}{l}y=f(x)=c\cdot e^{-qx}+\frac{s}{q}\\ y_0=f(0)=c+\frac{s}{q},alsoc=y_0-\frac{s}{q}\\ y=f(x)=(y_0-\frac{s}{q})\cdot e^{-qx}+\frac{s}{q}\end{array}$ (7)

Bestimmung für Gleichung (6):
$\begin{array}{l}\overline{y}=\overline{f}(x)=c´{(}^1+\frac{s}{q}\\ y_0=\overline{f}(0)=c´+\frac{s}{q},alsoc´=y_0-\frac{s}{q}\\ \overline{y}=\overline{f}(x)=(y_0-\frac{s}{q}){(}^1+\frac{s}{q}\end{array}$ (8)

Für die Parameterwerte $s=\mathrm{2,}q=1und{y}_0=0$ ergeben sich die Gleichungen
$y=f(x)=-2e^{-x}+2$ (9)
und
$\overline{y}=\overline{f}(x)=-2{(1-h)}^{\frac{x}{h}}+2$ (10).

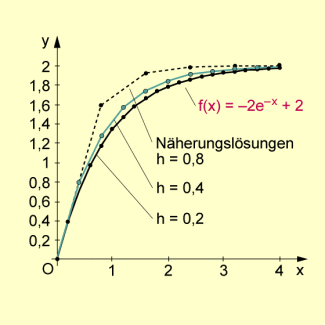
In der folgenden Abbildung sind die Lösung (9) sowie Näherungslösungen nach (10) mit $h=\mathrm{0,8,}h=\mathrm{0,4}undh=\mathrm{0,2}$ abgebildet. Je kleiner h wird, desto besser stimmt die Näherungslösung mit der exakten Lösung überein und desto höher ist der Rechenaufwand.