Betragsfunktion

Die Betragsfunktion ist eine stückweise erklärte stetige Funktion. Sie ist folgendermaßen definiert:
$f\left(x\right)=\{\begin{array}{c}x\text{für }x\ge 0\\ -x\text{für }x<0\end{array}$
Bild 1 zeigt den Graphen dieser Funktion.

Betrag einer Zahl

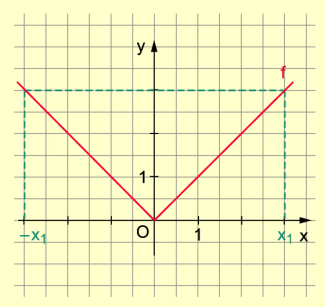
Im einfachsten Fall bedeutet der Betrag einer Zahl den Abstand dieser Zahl von der Stelle 0 der Zahlengeraden, wobei „Abstand“ stets als positive Zahl verstanden wird.

Es ist also:
$\left|+\mathrm{2,4}\text{‌}\right|=\left|-\mathrm{2,4}\text{‌}\right|=\mathrm{2,4}$
Gemäß obiger Definition der Betragsfunktion entspricht das Folgendem:
$\left|+\mathrm{2,4}\text{‌}\right|=\mathrm{2,4}und\left|-\mathrm{2,4}\text{‌}\right|=-\left(-\mathrm{2,4}\right)$

Betrag eines Terms

Ist der Betrag eines Terms zu bilden, der eine Unbekannte enthält, dann ist eine Fallunterscheidung erforderlich:

Für alle die Werte der Unbekannten, für die der Wert des Terms größer oder gleich null ist, können die Betragszeichen einfach fortgelassen werden.

Beispiele:
1. $\left|x^2+1\right|=x^2+1$,
weil $x^2+1$ für alle Werte von x positiv ist.

2. $\left|x+1\right|=x+1$ für $x\ge -1$,
da nur für der Term positiv bzw. gleich null ist.

Für alle die Werte der Unbekannten, für die der Wert des Terms kleiner null ist, können die Betragszeichen auch entfallen, allerdings ist der Term in Klammern einzuschließen und mit –1 zu multiplizieren.

Beispiele:
1. $\left|-x^2-1\right|=-\left(-x^2-1\right)$,
da der Term $-x^2-1$ für alle Werte von x negativ ist.

2. $\left|x+1\right|=-\left(x+1\right)$ für $x<-1$,
da für Werte $x<-1$ der Term $x+1$ negativ ist.

Graphen von Funktionen mit Beträgen

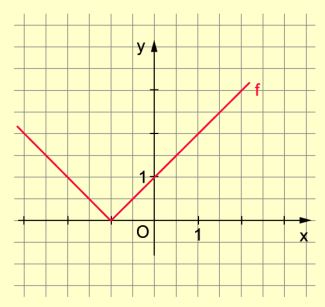
Nach den obigen Vorbetrachtungen hat die Funktion $y=f\left(x\right)=\left|x+1\right|$ folgenden Verlauf:

• $f\left(x\right)=x+1$ für $x\ge -1$
• $f\left(x\right)=-\left(x+1\right)=-x-1$ für $x<-1$

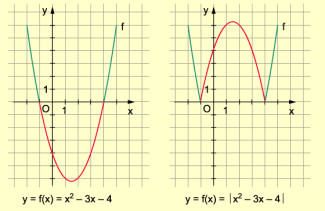
Wenn der Graph einer Funktion $y=f\left(x\right)$ sowohl oberhalb als auch unterhalb der x-Achse verläuft (die Funktion also positive und negative Werte annimmt), so werden durch $y=\left|f\left(x\right)\right|$ die unterhalb der x-Achse verlaufenden Teile des Graphen an der x-Achse gespiegelt.

Beispiel:
$y=f\left(x\right)=x^2-3x-4bzw.y=f\left(x\right)=\left|x^2-3x-4\right|$

Die Graphen weiterer Funktionen mit Beträgen können mit dem interaktiven Rechenbeispiel erzeugt werden.

Für Knobler:

Welche Punktmenge wird durch $\left|y\right|=\left|x+1\right|$ beschrieben?