Intervalle
Eine Menge reeller Zahlen nennt man Intervall, wenn sie sich auf der Zahlengeraden als Strecke darstellen lässt.
Gehören die Randwerte mit zum Intervall, spricht man von einem abgeschlossenen Intervall, gehören sie nicht zur dargestellten Menge, spricht man von einem offenen Intervall.
Eine Menge reeller Zahlen nennt man Intervall, wenn sie sich auf der Zahlengeraden, als Strecke darstellen lässt.
Gehören die Randwerte mit zum Intervall, spricht man von einem abgeschlossenen Intervall, gehören sie nicht zur dargestellten Menge, spricht man von einem offenen Intervall.
Die Intervallgrenzen werden zumeist mit eckigen Klammern oder Punkten gekennzeichnet (Bild 1).
-
Übersicht über Intervalle
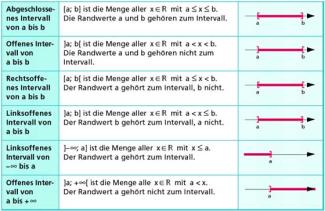
Intervallarten und Beispiele
abgeschlossenes Intervall
ist die Menge aller ; x ist größer bzw. gleich a und kleiner bzw. gleich b. Die Randwerte a und b gehören damit zum Intervall.
Beispiel (Bild 2):
Die Menge besteht aus allen rellen Zahlen zwischen –2 und 6, für die gilt . Sowohl –2 als auch 6 gehören zur Menge.
-
Abgeschlossenes Intervall

offenes Intervall
ist die Menge aller ; x ist größer a und kleiner b.
Die Randwerte a und b gehören damit nicht zum Intervall.
Beispiel (Bild 3):
Die Menge besteht aus allen rellen Zahlen zwischen –2 und 6, für die gilt . Sowohl –2 als auch 6 gehören nicht zur Menge.
ist die Menge aller ; x ist größer a.
Der Randwert a gehört nicht zum Intervall.
ist die Menge aller ; x ist kleiner b.
Der Randwert b gehört nicht zum Intervall.
-
Offenes Intervall

rechtsoffenes Intervall
ist die Menge aller ; x ist größer a bzw. gleich und kleiner b.
Der Randwert a gehört zum Intervall, und b gehört nicht zum Intervall.
Beispiel (Bild 4):
Die Menge besteht aus allen rellen Zahlen zwischen –2 und 6,
für die gilt . Die Zahl –2 gehört zur Menge, die Zahl 6 nicht.
ist die Menge aller ; x ist größer bzw. gleich a.
Der Randwert a gehört zum Intervall.
-
Rechtsoffenes Intervall

linksoffenes Intervall
ist die Menge aller ; x ist größer a und kleiner bzw. gleich b.
Der Randwert a gehört nicht zum Intervall und b gehört zum Intervall.
Beispiel (Bild 5):
Die Menge besteht aus allen rellen Zahlen zwischen –2 und 6, für die gilt . Die Zahl –2 gehört nicht zur Menge, die Zahl
6 gehört zur Menge.
ist die Menge aller ; x ist kleiner bzw. gleich b.
Der Randwert b gehört zum Intervall.
-
Linksoffenes Intervall


