Kugelteile
Wird eine Kugel durch eine Ebene oder mehrere Ebenen geschnitten, so entstehen verschiedene Schnittfiguren.
Beim Schnitt einer Kugel durch eine Ebene entstehen zwei Kugelabschnitte (Kugelsegmente). Verläuft diese Schnittebene genau durch den Kugelmittelpunkt, entstehen zwei Halbkugeln.
Wird eine Kugel durch eine Ebene oder mehrere Ebenen geschnitten, so entstehen verschiedene Schnittfiguren.
Beim Schnitt einer Kugel durch eine Ebene entstehen zwei Kugelabschnitte (Kugelsegmente). Verläuft diese Schnittebene genau durch den Kugelmittelpunkt, entstehen zwei Halbkugeln. Der jeweils abgetrennte Teil der Kugeloberfläche heißt Kugelkappe (Kugelhaube, Kalotte, Bild 1).
-
Kugelabschnitt
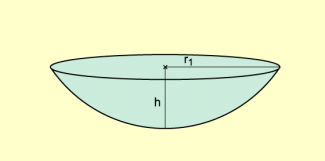
Für den Oberflächeninhalt eines Kugelabschnitts gilt:
Für das Volumen eines Kugelabschnitts gilt:
Eine Kugelschicht entsteht, wenn zwei zueinander parallele Ebenen eine Kugel schneiden (Bild 2). Aus der Oberfläche wird eine Kugelzone ausgeschnitten. Die Kugelschicht lässt sich als Differenz zweier Kugelabschnitte auffassen.
-
Kugelschicht
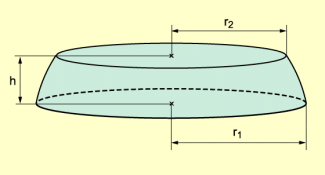
Für den Oberflächeninhalt einer Kugelschicht gilt:
Für das Volumen einer Kugelschicht gilt:
Ein Kugelausschnitt ( Kugelsektor) entsteht indem man alle Punkte einer Kugelkappe mit dem Mittelpunkt der Kugel verbindet (Bild 3). Das Volumen eines Kugelausschnitts entsteht aus der Summe eines Kugelabschnitts und eines Kreiskegels.
-
Kugelausschnitt
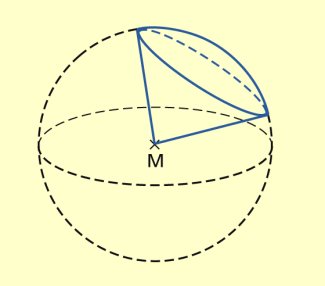
Für den Oberflächeninhalt eines Kugelausschnitts gilt:

