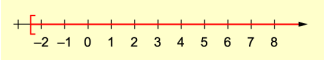Lineare Ungleichungen, mit einer Variablen
Zwei Terme, zwischen denen eines der Zeichen steht, bilden eine Ungleichung.
Ungleichungen der Form ax + b < 0 () oder solche, die durch äquivalentes Umformen in diese Form überführt werden können, heißen lineare Ungleichungen mit einer Variablen.
Zwei Terme, zwischen denen eines der Zeichen
steht, bilden eine Ungleichung.
Ungleichungen der Form ax + b < 0 () oder solche, die durch äquivalentes Umformen in diese Form überführt werden können, heißen lineare Ungleichungen mit einer Variablen.
Äquivalentes Umformen von Ungleichungen
- Das Addieren und das Subtrahieren derselben rationale Zahl auf beiden Seiten der Ungleichung
- Das Addieren und das Subtrahieren desselben Terms auf beiden Seiten der Ungleichung
- Das Multiplizieren und das Dividieren mit einer positiven rationalen Zahl auf beiden Seiten der Ungleichung
- Das Multiplizieren und das Dividieren mit einer negativen rationalen Zahl auf beiden Seiten der Ungleichung mit gleichzeitigem Umdrehen des Relationszeichens
Beispiel 1:
Die Lösungsmenge lässt sich auf der Zahlengeraden veranschaulichen (Bild 1).
-
Darstellung der Lösungsmenge auf der Zahlengeraden

Beispiel 2:
Die Lösungsmenge lässt sich auf der Zahlengeraden veranschaulichen (Bild 2).
-
Darstellung der Lösungsmenge auf der Zahlengeraden