Nullstellen
Jede Zahl x aus dem Definitionsbereich einer Funktion f, für die
f(x) = 0 gilt, nennt man Nullstelle dieser Funktion.
Bei Untersuchungen von Funktionen mit Gleichungen der Form werden meist zunächst Funktionswerte zu vorgegebenen Argumenten x, also die Werte der Funktion f an bestimmten Stellen x ermittelt. Aber auch die umgekehrte Fragestellung kann von Bedeutung sein, nämlich
- die Stellen x zu bestimmen, wo die Funktion f einen bestimmten gegebenen Wert besitzt,
- das Argument x zu einem gegebenen Funktionswert zu ermitteln,
- das erste Element bei einer als Paarmenge gegebenen Funktion zum jeweils zweiten Paarelement zu bestimmen,
- dasjenige Element des Definitionsbereichs zu ermitteln, das durch f auf ein gegebenes Element des Wertebereichs abgebildet wird,
-
Nullstelle einer linearen Funktion
oder (auf den Graphen von f bezogen)
die Abszisse x eines Punkts des Graphen von f zu bestimmen, der die Ordinate besitzt (interaktives Rechenbeispiel 1).
Beispiele:
- Man bestimmte die Stelle x, an der die Funktion f mit den Wert –4 besitzt.
Lösung:
Somit ist . - Man ermittle das Argument x zu dem Funktionswert 7 bei der Funktion .
Lösung:
Es gibt in diesem Falle zwei Argumente ( und ), die den Funktionswert 7 besitzen. - Es ist das Element x des Definitionsbereichs zu bestimmen, das durch die Funktion auf die Zahl 1 abgebildet wird.
Lösung:
Da es keine reelle Zahl gibt, deren Quadrat negativ ist, kann die Zahl 1 kein Element des Wertebereichs von f sein. - Es ist zu untersuchen, ob der Graph der Funktion f mit einen Punkt mit der Ordinate 10 besitzt.
Lösung:
Also ist x2 = 36 und damit x1 = 6 und x2 = –6 .
Die Punkte des Graphen von f mit den Abszissen x1 = 6 und x2 = –6 besitzen die Ordinate 10.
Von besonderem Interesse bei der Untersuchung einer Funktion sind häufig
- diejenigen Stellen, an der eine Funktion den Wert 0 besitzt, also
- diejenigen Argumente, welche den Funktionswert 0 haben oder
- diejenigen Punkte, in denen der Graph der Funktion die Abszissenachse schneidet oder berührt, also Punkte, die die Ordinate 0 haben.
- Jede Zahl x aus dem Definitionsbereich einer Funktion f, für die f(x) = 0 gilt, nennt man Nullstelle dieser Funktion.
Eine Nullstelle einer Funktion f ist zugleich die Abszisse eines Punktes, in dem der Graph von f die x-Achse schneidet.
Um die Nullstelle(n) einer Funktion f mit der Gleichung bzw. die Abszisse(n) ihres (ihrer) Schnittpunkte(s) mit der x-Achse zu bestimmen, muss man für y in der Funktionsgleichung die Zahl 0 einsetzen und die entstehende Bestimmungsgleichung lösen.
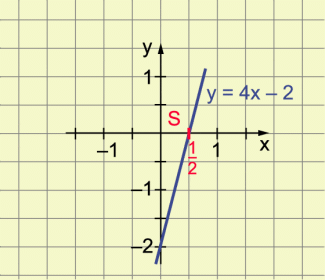
Beispiel 1 (Bild 1): Gegeben ist die Funktion mit der Gleichung . Gesucht sind der Schnittpunkt S ihres Graphen mit der x-Achse und die Nullstelle von f.
Lösung (für y = 0 eingesetzt):
Der Schnittpunkt des Graphen von f mit der x-Achse ist . Die Nullstelle ist .
Funktionsgraphen können keinen, einen oder mehrere Schnitt- bzw. Berührungspunkt(e) mit der x-Achse, die zugehörigen Funktionen also dann keine, eine oder mehrere Nullstelle(n) haben:
![]()
-
Nullstellen einer qudratischen Funktion
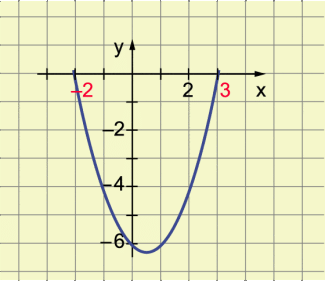
Beispiel 2 (Bild 2): Gesucht sind die Nullstellen der Funktion mit .
Lösung:
Es gibt zwei Nullstellen und .
Mit dem interaktiven Rechenbeispiel 2 können Nullstellen quadratischer Funktionen bestimmt werden, interaktives Rechenbeispiel 3 dient zur Ermittlung von Nullstellen beliebiger ganzrationaler Funktionen.

