Raute
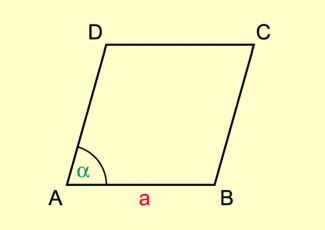
Ein Viereck mit vier gleich langen Seiten heißt Raute (Rhombus). Neben den Eigenschaften eines Parallelogramms (Parallelität der gegenüberliegenden Seiten) besitzt die Raute folgende Merkmale:
1. Die Seiten sind gleich lang.
2. Die Diagonalen stehen senkrecht aufeinander.
3. Die Diagonalen halbieren die Innenwinkel.
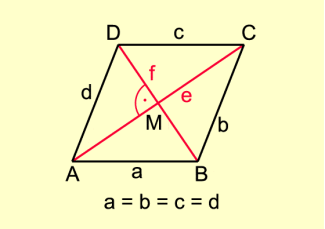
Ein Viereck mit vier gleich langen Seiten heißt Raut (Rhombus). Neben den Eigenschaften eines Parallelogramms (gegenüberliegende Seiten sind parallel, gegenüberliegende Winkel sind gleich groß) besitzt die Raute folgende Merkmale (Bild 1):
1. Die Seiten sind gleich lang.
2. Diagonalen stehen senkrecht aufeinander und halbieren einander.
3. Die Diagonalen halbieren die Innenwinkel.
-
Raute (Rhombus)
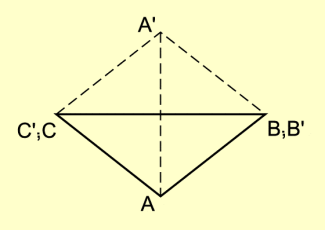
Eine Raute entsteht bei der Spiegelung eines gleichschenkligen (oder gleichseitigen) Dreiecks an der Basis (Bild 2). Damit ist eine Raute auch ein Spezialfall des Drachenvierecks.
Eine Raute besitzt zwei Symmetrieachsen und den Schnittpunkt der Diagonalen als Symmetriezentrum. Sie ist achsensymmetrisch und punktsymmetrisch.
-
Spiegelung eines Dreiecks
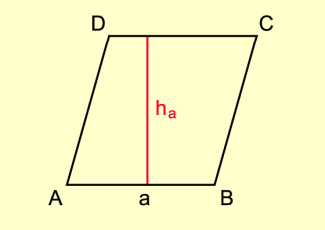
Da die Raute ein Sonderfall des Parallelogramms ist, lässt sich der Flächeninhalt nach folgender Formel bestimmen (Bild 3):
Ist ein Winkel der Raute ein rechter, so entsteht ein Quadrat. Beiden Vierecken ist gemeinsam, dass alle Seiten gleich lang sind. Für den Umfang einer Raute gilt (wie für den Umfang eines Quadrates):
u = 4 a
-
Flächeninhalt einer Raute
Die Konstruktion einer Raute ist bereits mit zwei Angaben möglich.
Beispiel:
Gegeben sind die Seite a und der Winkel (Bild 4).
- Auf einer Geraden wird die Strecke AB mit gezeichnet.
- In A wird der Winkel angetragen.
- Um A wird ein Kreisbogen mit dem Radius a gezeichnet. Man erhält den Punkt D.
- Um B und D wird jeweils einen Kreisbogen mit dem Radius a gezeichnet. Der Schnittpunkt der Kreisbogen ist C.
- D und B werden mit C zur Raute ABCD verbunden.
-
Raute