Satz des Thales

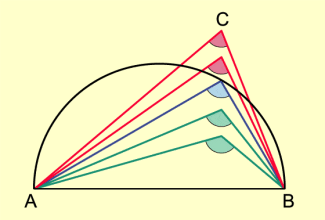
Zeichnet man den Durchmesser eines Kreises und mehrere Dreiecke ABC, deren dritter Eckpunkt innerhalb, außerhalb oder genau auf der Kreislinie liegt, so stellt man fest, dass der Winkel BCA von innen nach außen immer kleiner wird. Zuerst ist er stumpf, dann ist er spitz. In einem Fall tritt ein rechter Winkel auf (Bild 1).

THALES VON MILET ( um 624 bis 548 v. Chr.) hat als erster griechischer Mathematiker der Antike allgemeine Aussagen für mathematische Objekte aufgestellt und in Ansätzen logische Begründungen dafür angegeben. Er zählt damit neben seinem Schüler PHYTHAGORAS zu den Wegbereitern einer neuen Entwicklungsetappe der Mathematik.
Als er bei einem Aufenthalt in Ägypten herausfand, dass man um ein rechtwinkliges Dreieck immer einen Kreis zeichnen kann, opferte er für diese Entdeckung einen Ochsen.

Satz des Thales

Jeder Umfangswinkel über einem Halbkreis (bzw. über dem Durchmesser eines Kreises) ist ein rechter Winkel.

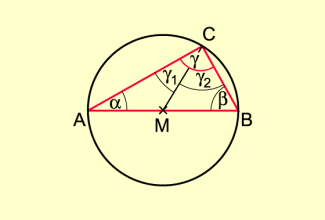
Beweis (mithilfe der Winkelsumme in gleichschenkligen Dreiecken, Bild 3)
Voraussetzung:
A, B und C liegen auf dem Kreis um M.
AB ist Durchmesser des Kreises.

Behauptung:
$\gamma =90°$

Beweis:
Es gilt: $\alpha ={\gamma }_{1}und\beta ={\gamma }_2$ (Basiswinkel in den gleichschenkligen Dreiecken AMC und MBC)
Es folgt daraus: $\alpha +\beta ={\gamma }_1+{\gamma }_2=\gamma$
Da auch $\alpha +\beta +\gamma =180°$ (Winkelsumme im Dreieck) gilt , ist $2\cdot \gamma =180°$ bzw. $\gamma =90°$. (w. z. b. w.)

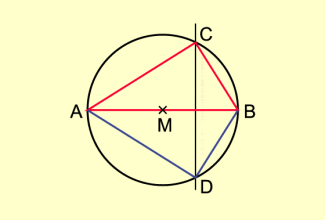
Beweis (mithilfe der Spiegelung des Dreiecks ABC, Bild 4)
Das Dreieck ABC wird an AB gespiegelt. Dabei ist das Bild von C der Punkt D.
Das Viereck ADBC ist Sehnenviereck. Deshalb ergänzen sich die Winkel in D und in C zu $180°$.
Weil der Winkel in D das Bild des Winkels in C bei der Spiegelung an AB ist, sind beide Winkel zueinander kongruent und damit rechte Winkel.

Umkehrung des Thalessatzes

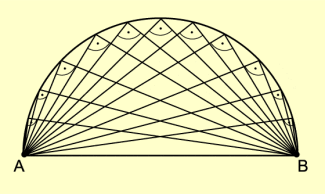
Wenn man eine Reihe von rechtwinkligen Dreiecken mit der gleichen Hypotenuse $\overline{AB}$ zeichnet, so lässt sich leicht die Vermutung gewinnen, dass alle Eckpunkte C auf einem Kreis liegen. Diese richtige Vermutung stellt die Umkehrung des Thalessatzes dar, die sich durch Vertauschen von Voraussetzung und Behauptung ergibt (Bild 5).

Ist ein Dreieck ABC rechtwinklig mit dem rechten Winkel bei C, dann liegt C auf dem Kreis mit dem Durchmesser $\overline{AB}$. Dieser Kreis heißt auch Thaleskreis.

Anwendungen des Thalessatzes beim Lösen von Konstruktionsaufgaben

Wenn man sagt, eine Strecke $\overline{AB}$ erscheint von einem Punkt P aus unter einem Winkel $\gamma$, so ist damit der Winkel BPA gemeint.
Durch die Umkehrung des Thalessatzes ergibt sich:
Die Menge aller Punkte, von denen aus eine Strecke $\overline{AB}$ unter einem Winkel $90°$ von erscheint, ist ein Kreis mit $\overline{AB}$ als Durchmesser.

Der Thaleskreis kann als Bestimmungslinie für Punkte verwendet werden, die Scheitelpunkt eines rechten Winkels sind (Bild 6).

Beispiel:
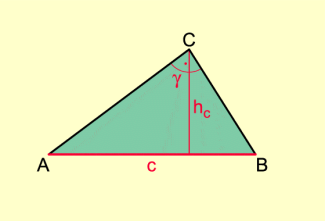
Von einem Dreieck sind c, $h_c$ und $\gamma =90°$ gegeben.
Konstruktionsbeschreibung:
Die Punkte A und B sind durch c festgelegt.
Der Punkt C liegt:
1. auf dem Thaleskreis über $\overline{AB}$ und
2. auf einer Parallelen zu $\overline{AB}$ im Abstand $h_c$.

Beispiel:
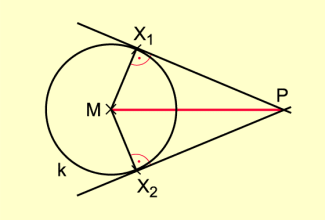
Es sollen die Tangenten an einen Kreis k durch einen Punkt P außerhalb des Kreises konstruiert werden (Bild 7).

Vorbemerkungen:
Es sind die Berührungspunkte $X_1$ und $X_2$ der Tangenten gesucht.
Es gilt $\sphericalangle P{X}_{1}M=90°$ bzw. $\sphericalangle M{X}_{2}P=90°$, da Tangente und Berührungsradius senkrecht zueinander sind.

Konstruktionsbeschreibung:
Der Punkt X liegt:
1. auf dem Kreis k und
2. auf dem Thaleskreis mit dem Durchmesser $\overline{PM}$.