Adiabatische Zustandsänderungen

Zustandsänderungen von Gasen sind im Allgemeinen komplizierte, komplexe Vorgänge. So wird beispielsweise in Verbrennungsmotoren das Kraftstoff-Luftgemisch so schnell verdichtet, dass kaum ein Wärmeaustausch mit der Umgebung erfolgt. Dieser Teilprozess kann also als adiabatischer Prozess angesehen werden.
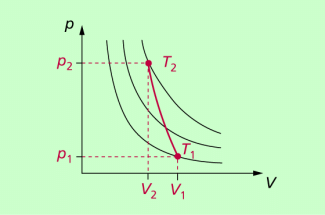
Charakteristisch für adiabatische Vorgänge ist, dass sich alle drei Zustandsgrößen Temperatur, Druck und Volumen gleichzeitig ändern. Die Adiabate im p-V-Diagramm verläuft steiler als Isothermen und schneidet diese (Bild 1).

Je nach der Richtung der Zustandsänderung kann man zwischen einer adiabatischen Expansion und einer adiabatischen Kompression unterscheiden.

adiabatische Expansion: Das Gas expandiert, das Volumen wird größer. Dabei verringert sich die innere Energie des Gases, die Temperatur und der Druck des Gases sinken. Die Änderung der inneren Energie U ist gleich der vom System verrichteten Arbeit W (W < 0). Mit Q = 0 erhält man aus dem 1. Hauptsatz der Thermodynamik:

$\Delta U=W$

adiabatische Kompression: Das Gas wird komprimiert. Dazu wird äußere Arbeit (W > 0) verrichtet, das Volumen verringert sich, die dabei entstehende Wärme wird vollständig in innere Energie des Gases umgewandelt. Die Temperatur und der Druck erhöhen sich. Es gilt nach dem 1. Hauptsatz der Thermodynamik:

$W=\Delta U$

Weitere quantitative Zusammenhänge

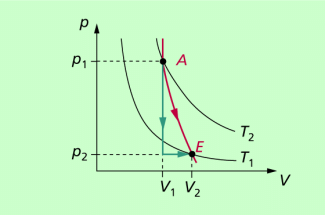
Bei Verwendung des Modells ideales Gas kann die Adiabate p = p(V) berechnet werden. Dazu wird der adiabatische Übergang von einem Anfangszustand A in einen Endzustand E (adiabatische Expansion) in zwei Teilprozesse zerlegt (Bild 2). Die Verringerung des Druckes von $p_1\text{auf}{p}_2$ erfolgt isochor (V = konstant) und die Volumenänderung von $V_1\text{auf}{V}_2$ in einem isobaren Vorgang (p = konstant). Beide Prozesse laufen gleichzeitig ab und verringern die Temperatur des Gases von $T_1\text{auf}{T}_{\text{2}}.$
Durch die isochore Zustandsänderung des Gases wird die innere Energie des Gases verringert, seine Temperatur sinkt um $\Delta T_{\text{V}}$.
Die innere Energie U des Gases im Ausgangszustand A ist:

$\begin{array}{l}U=\frac{3}{2}N\cdot k\cdot T_1\\ N\text{Teilchenanzahl}\\ k\text{BOLTZMANN-Konstante}\\ T\text{absolute Temperatur}\end{array}$

Während des isochoren Teilvorgangs ändert sich die Temperatur des Gases um $\Delta T_{\text{V}}$ und die innere Energie um. Die innere Energie im Endzustand E ist daher:
$U+\Delta U=\frac{3}{2}N\cdot k\cdot (T_1+\Delta T_{\text{V}})$
Daraus ergibt sich für die Änderung der inneren Energie:
$\Delta U=\frac{3}{2}N\cdot k\cdot \Delta T_{\text{V}}$
Für die Änderung der inneren Energie einer isochoren Zustandsänderung kann man unter Nutzung der Masse und der spezifischen Wärmekapazität bei konstantem Druck auch schreiben:

$\Delta U=m\cdot c_{\text{p}}\cdot \Delta T_{\text{V}}$

Die Verringerung der Temperatur bei der isochore Zustandsänderung ist mit einer Abnahme des Druckes verbunden. Den Zusammenhang zwischen Temperatur- und Druckänderung gibt die Zustandsgleichung des idealen Gases an. Bei konstantem Volumen ist:
$V\cdot \Delta p=N\cdot k\cdot \Delta T_{\text{V}}$

Durch Umformen der genannten Gleichung nach $\Delta T_{\text{V}}$ und Einsetzen in die vorher genannte Gleichung für die Änderung der inneren Energie folgt für die Änderung der inneren Energie des isochoren Teilvorgangs:
$\Delta U=\frac{m\cdot c_{\text{v}}}{N\cdot k}\cdot V\cdot \Delta p$

Diese Energie, die dem Gas entzogen wird, entspricht exakt der Wärme, die zur Realisierung des isobaren Teilprozesses notwendig ist.

Bei der isobaren Zustandsänderung (isobare Expansion), dem zweitem Teilprozess, wird das Volumen von $V_1\text{auf}{V}_2$ vergrößert. Dazu verrichtet das Gas Volumenarbeit. Die Vergrößerung des Volumens bei konstantem Druck ist mit einer Änderung der Temperatur und damit auch mit einer Änderung der inneren Energie verbunden. Die vom Gas verrichtete Volumenarbeit bei der isobaren Expansion ist:
$W=-p\cdot \Delta V=-N\cdot k\cdot \Delta T_{\text{p}}$

Bei der Erhöhung der Temperatur ändert sich auch die innere Energie eines idealen Gases um:

$\Delta U=\frac{3}{2}N\cdot k\cdot \Delta T_{\text{p}}$

Aus dem 1. Hauptsatzes kann damit die Wärme bestimmt werden, die für die Realisierung des isobaren Teilprozesses notwendig ist.
$Q=\frac{3}{2}N\cdot k\cdot \Delta T_{\text{p}}+N\cdot k\cdot \Delta T_{\text{p}}=\frac{5}{2}N\cdot k\cdot \Delta T_{\text{p}}$
$\begin{array}{l}\text{Durch Einführung der molaren Wärmekapazitäten}\\ \text{bei konstantem Druck}{C}_{\text{mp}}=\frac{5}{2}R\text{und der spezifischen}\\ \text{Wärmekapazität bei konstantem Druck}{c}_{\text{p}}=\frac{C_{\text{mp}}}{M}\\ \text{folgt für die Wärme Q:}\\ Q=n\cdot C_{\text{mp}}\cdot \Delta T_{\text{p}}=m\cdot c_{\text{p}}\cdot \Delta T_{\text{p}}\end{array}$

Den Zusammenhang zwischen Temperatur- und Volumenänderung gibt die Zustandsgleichung des idealen Gases an. Bei konstantem Druck ist:
$p\cdot \Delta V=N\cdot k\cdot \Delta T_{\text{p}}$

Durch Ersetzen von $\Delta T_{\text{p}}$ folgt für die Wärme, die für den isobaren Teilvorgang notwendig ist:
$Q=\frac{m\cdot c_{\text{p}}}{N\cdot k}\cdot p\cdot \Delta V$

Zur Berechnung der Adibate p = p (V) müssen beide Teilvorgänge im Zusammenhang betrachtet werden. Die Verringerung der inneren Energie bei der isochoren Zustandsänderung steht zur Realisierung der isobaren Expansion zur Verfügung. Daraus ergibt sich die Bilanz
$Q=-\frac{m\cdot c_{\text{p}}}{N\cdot k}\cdot p\cdot \Delta V=\frac{m\cdot c_{\text{V}}}{N\cdot k}\cdot V\cdot \Delta p=\Delta U$
Durch Vereinfachung und Einführung des Adiabatenexponenten $\kappa$ (auch Adiabatenkoeffizient oder POISSON-Konstante genannt) mit
$\kappa =\frac{c_{\text{p}}}{c_{\text{V}}}$
erhält man daraus die Gleichung:

$\kappa \cdot \frac{\Delta V}{V}+\frac{\Delta p}{p}=0$
Nach Übergang zu infinitisimalen Größen kann die Gleichung integriert werden.

$\begin{array}{l}\kappa \cdot {\displaystyle \int \frac{\text{d}V}{V}}+{\displaystyle \int \frac{\text{d}p}{p}}=0\\ \kappa \cdot \ln V+\ln p=\ln C\end{array}$

C ist dabei eine Integrationskonstante. Durch Umformung unter Nutzung der Logarithmengesetze ergibt sich daraus ein Gesetz, das als poissonsches Gesetz (benannt nach dem französischen Mathematiker und Physiker SIMÉON DENIS POISSON, der von 1781-1840 lebte) bezeichnet wird und folgendermaßen geschrieben werden kann:

$p\cdot V^{\kappa }=\text{konstant}\text{oder}{p}_1\cdot V_1^{\kappa }=p_2\cdot V_2^{\kappa }$

Wird die Zustandsgleichung für ideale Gase verwendet, so lässt sich diese Gleichung weiter umformen. Es ergeben sich die poissonschen Gesetze in der Form:

$\frac{T_2}{T_1}={\left(\frac{V_1}{V_2}\right)}^{\kappa -1}\text{oder}\frac{T_2}{T_1}={\left(\frac{p_1}{p_2}\right)}^{\frac{\kappa -1}{\kappa }}$

Auf dem Bild werden ein Ausgangszustand A und ein Endzustand E betrachtet. Der adiabatische Prozess (rote Linie) kann „ersetzt“ werden durch einen isochoren Prozess (senkrechte grüne Linie) und einen isobaren Prozess (waagerechte grüne Linie).