Verbundene Gefäße

Verbundene Gefäße sind Anordnungen von Gefäßen, die aus mehreren Teilen bestehen, wobei diese Teile miteinander verbunden sind. Daher stammt auch die Bezeichnung. Die Flüssigkeit steht in allen Teilen des verbundenen Gefäßes gleich hoch, unabhängig davon, welche Form diese Teile haben. Diese Erscheinung wird als hydrostatisches Paradoxon bezeichnet.

Warum stehen die Flüssigkeitssäulen überall gleich hoch?

Eine Erklärung für die gleiche Höhe der Flüssigkeitssäule in den verschiedenen Teilen des verbundenen Gefäßes ergibt sich aus Betrachtungen zum Schweredruck, den die jeweiligen Flüssigkeitssäulen ausüben: In einer bestimmten Tiefe müssen sich die Drücke, die infolge der Gewichtskraft der Flüssigkeitssäulen wirken, ausgleichen. Da der Druck nur von der Höhe der Flüssigkeitssäule, nicht aber von der Gefäßform abhängig ist, müssen bei einer Flüssigkeit die Säulen in allen Teilen des verbundenen Gefäßes gleich hoch stehen.

Anwendungen

Um zu sichern, dass z. B. Mauern gleich hoch sind, nutzt man auf Baustellen Schlauchwaagen (Bild 3). Eine solche Schlauchwaage besteht aus zwei röhrenförmigen Gefäßen, die mit einem Schlauch verbunden und mit Wasser gefüllt sind. Da die Flüssigkeitssäule in beiden Gefäßen gleich hoch steht, kann man mit der Schlauchwaage feststellen, ob z. B. eine Mauer an verschiedenen Stellen tatsächlich gleich hoch ist.

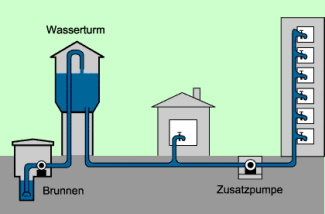
Bei Wasserversorgungsanlagen (Bild 4) nutzt man ebenfalls, dass Wasser in verbundenen Gefäßen gleich hoch steht, unabhängig davon, welche Form diese Gefäße haben. Um eine stabile Wasserversorgung zu sichern, wird Wasser in einen Wasserturm gepumpt. Es gelangt damit zu allen Zapfstellen, die eine geringere Höhe als der Wasserspiegel im Wasserturm haben. Für Hochhäuser oder Gebäude, die über diesem Wasserspiegel liegen, sind Zusatzpumpen erforderlich.

Um den Füllstand von undurchsichtigen Behältern mit Flüssigkeit kontrollieren zu können, verwendet man Füllstandsanzeiger (Bild 5). Das ist ein durchsichtiges Glas- oder Plastikröhrchen, das mit dem Behälter verbunden ist und mit ihm ein verbundenes Gefäß bildet. Die Flüssigkeit steht in dem Anzeigeröhrchen und im Behälter gleich hoch. Damit kann man den jeweiligen Füllstand kontrollieren.

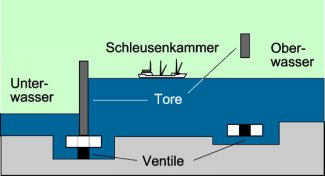
Auch bei einer Schleuse bildet je nach Stellung der Tore die Schleusenkammer mit dem Unterwasser oder dem Oberwasser ein verbundenes Gefäß (Bild 6). Durch unterschiedliches Öffnen und Schließen der Toren und Ventile wird das hydrostatische Paradoxon genutzt, dass in verbundenen Gefäßen Flüssigkeitssäulen gleich hoch stehen. Ist z. B. das obere Tor geöffnet und das untere Tor geschlossen, so kann ein Schiff aus dem oberen Wasser in die Schleusenkammer einfahren. Dabei muss das untere Ventil geschlossen sein. Dann wird nach Schließen des oberen Tors und es Ventils das untere Ventil geöffnet. Das Wasser kann aus der Schleusenkammer in den unteren Wasserlauf abfließen. Der Wasserspiegel mit dem Schiff senkt sich so weit, bis er genau so hoch ist wie das Unterwasser. Das Schiff kann ausfahren. Beim Hochschleusen müssen die Tore und Ventile in der umgekehrten Reihenfolge geöffnet und geschlossen werden.