Gravitationsgesetz

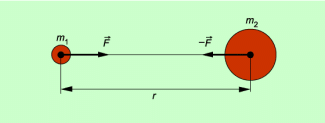
Zwei Körper ziehen sich aufgrund ihrer Masse gegenseitig an. Diese Erscheinung wird als Massenanziehung oder Gravitation bezeichnet. Die dabei wirkenden Kräfte bezeichnet man als Gravitationskräfte.
Die Gravitationskraft zwischen zwei Körpern ist umso größer,

• je größer die Massen der Körper sind und
• je kleiner der Abstand ihrer Massenmittelpunkte voneinander ist.

Der Betrag der Kraft kann mit dem Gravitationsgesetz berechnet werden. Es lautet:

$\begin{array}{l}F=G\cdot \frac{m_1\cdot m_2}{r^2}\\ G\text{ Gravitationskonstante}\\ m_1,m_2\text{ Massen der Körper}\\ r\text{ Abstand der Massenmittelpunkte}\\ \text{ der beiden Körper voneinander}\end{array}$

Dieses Gesetz wurde von dem englischen Physiker ISAAC NEWTON (1643-1727) entdeckt. Es gilt nicht nur für die Erde und die auf ihr befindlichen Körper, sondern für beliebige Körper, die eine Masse besitzen, z. B. auch für die Sonne oder andere Himmelskörper. Die im Gesetz genannte Gravitationskonstante ist eine Naturkonstante. Sie hat einen Wert von:

$G=\mathrm{6,673}\cdot {10}^{-11}{\text{ m}}^{\text{3}}\cdot {\text{kg}}^{\text{-1}}\cdot {\text{s}}^{\text{-2}}$

Mithilfe des Gravitationsgesetzes ist es möglich zu berechnen, mit welcher Kraft die Erde einen Körper anzieht, der sich auf ihrer Oberfläche befindet. Es ist auch möglich zu berechnen, mit welcher Kraft die Erde den Mond anzieht oder mit welcher Kraft die Erde von der Sonne angezogen wird.
Das nachfolgende Bild zeigt schematisch das Kräftegleichgewicht zwischen Mond (m₁) und Erde (m₂).