Saugpumpe

Handbetriebene Pumpen für Wasser sind meist Saugpumpen. Bild 1 zeigt eine mögliche Bauform.
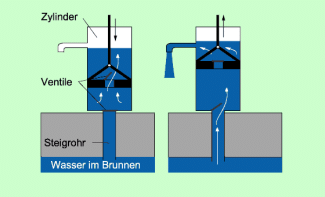
Der Aufbau einer solchen Saugpumpe ist in Bild 2 dargestellt. Sie besteht aus einem Zylinder, in dem sich ein Kolben mit Ventil befindet. Bewegt wird dieser Kolben mit dem Pumpenschwengel. Darüber hinaus existiert eine Verbindung zum Brunnen in Form eines Steigrohres, das von der Pumpe ebenfalls durch ein Ventil getrennt ist.

Beim Abwärtsbewegen des Kolbens (Bild 2a) ist das Ventil im Kolben geöffnet, das am Steigrohr geschlossen. Dadurch strömt Wasser in den Bereich oberhalb des Pumpenkolbens.
Beim Aufwärtsbewegen des Kolbens ist das Ventil im Kolben geschlossen. Das Wasser, das sich oberhalb des Kolbens befindet, wird gehoben und strömt durch den Ausfluss. Gleichzeitig entsteht durch diese Kolbenbewegung im Raum unterhalb des Kolbens ein Unterdruck. Wasser strömt durch das Ventil im Steigrohr nach.

Die Ursache für das Nachströmen des Wassers ist der Druckunterschied zwischen dem Raum unterhalb des Kolbens (Unterdruck) und dem Wasser im Brunnen. Auf dieses Wasser wirkt in der Regel der Luftdruck. Damit strömt nur dann Wasser nach, wenn der Luftdruck größer ist als der Druck, den die Wassersäule im Steigrohr und unterhalb des Pumpenkolbens ausübt. Die theoretisch mögliche maximale Förderhöhe solcher Saugpumpen ergibt sich damit aus der Länge der Wassersäule, die einen Druck ausübt, der gleich dem Luftdruck ist. Diese Länge beträgt 10,33 m.

Die Erfahrung von Brunnenbauern, dass Wasser mit einfachen Pumpen höchstens aus einer Tiefe von 10 m gefördert werden kann, war für GALILEO GALILEI (1564-1642) und seinen Schüler EVANGELISTA TORRICELLI (1608-1647) entscheidender Anstoß dafür, sich genauer mit dem Luftdruck und seiner Größe zu beschäftigen. TORRICELLI stellte dabei fest, dass der Luftdruck gleich dem Druck von 760 mm Quecksilbersäule (= 760 Torr) entspricht. Der Magdeburger Bürgermeister und Forscher OTTO VON GUERICKE (1602-1686) maß den Luftdruck mit einer Wassersäule, die ca. 10 m hoch war.