Berechnung von Elektrodenpotenzialen mit der nernstschen Gleichung
Mithilfe der nernstschen Gleichung kann das Elektrodenpotenzial beliebiger Elektroden aus der ablaufenden Redoxreaktion berechnet werden. Das Elektroden- bzw. Redoxpotenzial ist ein Maß für das Oxidationsvermögen des Oxidationsmittels in wässriger Lösung. Es ist abhängig vom betrachteten Redoxpaar, den Konzentrationen der an der Redoxreaktion beteiligten Komponenten, der Temperatur und dem Druck (Gaselektroden). Je nach Art des Potenzial bestimmenden Schritts der Redoxreaktion unterscheidet man verschiedene Arten von Elektroden.
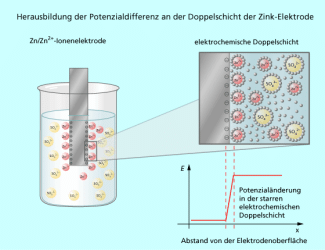
An einer elektrochemischen Doppelschicht einer Elektrode oder zwischen zwei Elektrolytlösungen eines Redoxpaars bildet sich eine Potenzialdifferenz E heraus. Diese kann man zwar nicht direkt messen, da nur ein Pol vorhanden ist, aber nach WALTHER H. NERNST (Bild 1) theoretisch berechnen. Für ein beliebiges Redoxpaar gilt die folgende Elektrodenreaktion mit der dazugehörigen nernstschen Gleichung:
Da elektrochemische Reaktionen spezielle Redoxreaktionen sind, bezeichnet man E sowohl als Elektrodenpotenzial als auch als Redoxpotenzial. Entsprechend der obigen Gleichung hängt E von folgenden Größen ab:
| 1. | von den chemischen Eigenschaften des Redoxpaars, d. h. vom Oxidationsvermögen des Oxidationsmittels (Standardelektrodenpotenzial ) und von der Anzahl z der bei der Redoxreaktion ausgetauschten Elektronen (Rechenbeispiel). |
| 2. | von der Temperatur, bei der die Reaktion stattfindet. Im konzentrationsabhängigen Teil der nernstschen Gleichung ist diese Temperaturabhängigkeit offensichtlich. Aber auch das Standardpotenzial ist temperaturabhängig und deshalb für eine Temperatur von 25 °C tabelliert. |
| 3. | von der Konzentration der an der Redoxreaktion beteiligten Komponenten. Diese Konzentration geht logarithmisch in das Elektrodenpotenzial ein (Rechenbeispiel). |
| 4. | bei Redoxreaktionen in wässriger Lösung, an denen Gase beteiligt sind, hängt das Standardelektrodenpotenzial außerdem noch vom Druck ab. Der Standarddruck für tabellierte Werte von beträgt 101,325 kPa. |
Betrachten wir als einfachen Fall eine Metallelektrode 1. Art, bei der ein Metall, z. B. ein Zinkblech, in Kontakt mit einer entsprechenden wässrigen Metallsalzlösung, z. B. Zinksulfat, steht (Bild 2). Die Potenzialdifferenz E zwischen der festen Phase und der Salzlösung wird hauptsächlich durch die Art des Metalls und der Metall-Ionen bestimmt. Das Bestreben der Metallatome, Elektronen abzugeben und in die wässrige Lösung überzugehen, hängt in der Regel von ihrer Ioniserungsenergie im PSE und der Hydratationsenthalpie der gebildeten Ionen ab. Zink gibt relativ leicht 2 Elektronen ab und das -Ion lässt sich gut hydratisieren, sodass das Standardpotenzial relativ niedrig ist. Das Standardelektrodenpotenzial ist demzufolge eine stoffspezifische, thermodynamische Größe und für jedes Redoxpaar unterschiedlich. Standardpotenziale sind unter Standardbedingungen für alle Redoxpaare gemessen worden und in sogenannten Spannungsreihen tabelliert.
Der zweite Summand in der nernstschen Gleichung beschreibt den Einfluss der Konzentration der Reaktionspartner auf das Elektrodenpotenzial. Je höher die Konzentration an -Ionen in wässriger Lösung ist, um so positiver wird das Elektrodenpotenzial E. Damit steigt die Tendenz zur Abscheidung von Zink. Der Zusammenhang zwischen Elektrodenpotenzial und Konzentration ist ebenfalls temperaturabhängig. Die Temperatur geht direkt in den konzentrationsabhängigen Summanden mit ein. Gleiches gilt für die Anzahl der bei der Elektrodenreaktion ausgetauschten Elektronen.
Die Konzentrationen c(i) in der nernstschen Gleichung müssen immer auf die Standardkonzentrationen normiert werden, damit man einheitenlose Quotienten erhält, die logarithmiert werden können. Daraus ergibt sich eine wichtige Vereinfachung, denn für reine feste Phasen (z. B. Metalle oder schwer lösliche Salze) und flüssige Phasen (z. B. Wasser) ist dieser Quotient 1. Deshalb tauchen diese Konzentrationen in den nernstschen Gleichungen so gut wie nie auf.
Eine weitere Vereinfachung ergibt sich, wenn man das Elektrodenpotenzial bei der Standardtemperatur von 25 °C bzw. 298,15 K betrachtet. In diesem Fall hängt der zweite Summand in der nernstschen Gleichung nur noch von der Anzahl der ausgetauschten Elektronen und der Konzentration der Metall-Ionen ab. Da häufiger mit dem dekadischen Logarithmus von Ionenkonzentrationen gerechnet wird, z. B. beim pH-Wert, rechnet man auch den natürlichen Logarithmus noch in den dekadischen um, indem man einfach mit 2,303 multipliziert.
Heraus kommt eine Gleichung, in der das Elektrodenpotenzial nur noch von der Art, Ladung und Konzentration des betrachteten Metalls bzw. der Metall-Ionen abhängt. Der Proportionalitätsfaktor von 59,2 mV ergibt sich aus den Naturkonstanten R und F sowie aus der Standardtemperatur.
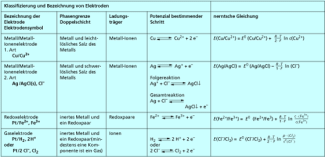
Auf ähnliche Weise lässt sich die nernstsche Gleichung für alle Elektroden bzw. für alle Redoxpaare herleiten. Die Redoxreaktion, die zur Ausbildung der Potenzialdifferenz führt, bezeichnet man als Potenzial bestimmenden Schritt . Danach kann man verschiedene Elektrodenarten unterteilen (Bild 3).
Eine wichtige Elektrodenart sind die Elektroden 2. Art, bei denen das Metall in Kontakt mit der gesättigten Lösung eines schwer löslichen Salzes steht. Ein Beispiel sind Ag/AgCl- oder , die sogenannte Kalomelelektrode. Die mathematische Ableitung des Elektrodenpotenzials ist in Bild 4 dargestellt. Bei beiden Elektroden verringert sich das Elektrodenpotenzial mit steigender Chlorid-Ionenkonzentration und erreicht in einer gesättigten Chlorid-Ionenlösung seinen jeweils kleinsten Wert. Folgende Elektrodenpotenziale bei einer Temperatur von 25 °C (298,15 K) erhält man für diese Elektroden 2. Art:
![]()
Relativ gering ist der Einfluss der Temperatur auf das Elektrodenpotenzial dieser Elektroden 2. Art. Für die Kalomelelektrode in einer 0,1 molaren Chlorid-Ionenlösung ergaben experimentelle Messungen folgende Abhängigkeit:
Das bedeutet, das sich das Elektrodenpotenzial in der Nähe der Standardtemperatur nur um ca. 0,1 mV je Kelvin ändert. Aufgrund dieses beinahe temperaturunabhängigen und weitgehend konzentrationsunabhängigen Elektrodenpotenzials werden Elektroden 2. Art bevorzugt als Bezugselektroden eingesetzt. Das bedeutet, sie werden mit anderen Elektroden in einer elektrochemischen Zelle zusammengeschaltet und aus der gemessenen Zellspannung kann das Potenzial der anderen Elektrode berechnet werden.
Eine weitere wichtige Elektrodenart sind Redoxelektroden , bei denen in wässriger Lösung eine Redoxreaktion stattfindet. Die Elektronen treten als Ladungsträger durch die Phasengrenze zwischen Lösung und dem an der Redoxreaktion unbeteiligten Metall der Elektrode. Beispiele für Redoxelektroden ist eine Eisen(II)-Salzlösung, in die ein Platindraht eintaucht, oder eine Kaliumpermanganatlösung, in die ein Grafitstift eintaucht. Das Potenzial dieser Elektroden wird ebenfalls durch die nernstsche Gleichung berechnet und enstpricht dem Redoxpotenzial der Lösung (Bild 5). Das Redoxpotenzial ist ein Maß für das Oxidationsvermögen des Oxidationsmittels in wässriger Lösung. Die Begriffe Redoxpotenzial und Elektrodenpotenzial werden als Synonyme für die gleiche Größe benutzt. Allerdings ist für wässrige Lösungen ohne Elektroden der Begriff Redoxpotenzial korrekter.