Ableitung der Sinusfunktion
Im Folgenden wird gezeigt, dass die Sinusfunktion im gesamten Definitionsbereich differenzierbar ist und die Ableitungsfunktion besitzt.
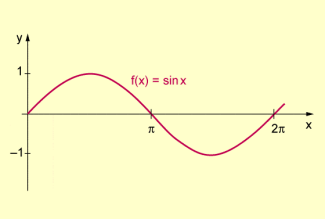
Dazu betrachten wir den Graph der Sinusfunktion im Intervall von 0 bis .
-
Graph der Sinusfunktion
Um die Ableitung der Sinusfunktion zu ermitteln, stellen wir den Differenzenquotienten von f an einer beliebigen Stelle auf:
Da nach einem Additionstheorem gilt, erhalten wir im vorliegenden Fall und damit:
Nun wird der Grenzwert des Differenzenquotienten für gebildet. Man erhält nach den Grenzwertsätzen:
Das bedeutet: Der Grenzwert des Differenzenquotienten für existiert, wenn die Grenzwerte existieren.
Es lässt sich zeigen, dass gilt.
Um ermitteln zu können, wird folgende Umformungen durchgeführt:
Wegen gilt
Damit ist
Für erhält man dann:
Setzt man die ermittelten Grenzwerte in obige Gleichung (*) ein, so ergibt sich: Der Grenzwert des Differenzenquotienten von an einer beliebigen Stelle existiert und es ist
Also gilt für die Ableitung der Sinusfunktion:
- Die Sinusfunktion ist im gesamten Definitionsbereich differenzierbar und besitzt die Ableitungsfunktion
Beispiel: Es ist der Anstieg der Funktion an der Stelle zu ermitteln.
Wir erhalten:
Damit gilt:

