Affine Abbildungen
Eine punktweise Abbildung der Ebene auf sich, die Geraden in Geraden überführt, parallele Geraden in parallele Geraden überführt und teilverhältnistreu ist, heißt affine Abbildung oder Affinität.
Beispiele für Affinitäten sind die Kongruenz- und Ähnlichkeitsabbildungen.
Begriff der Abbildung
Unter einer (geometrischen) Abbildung T der (Zeichen-)Ebene E auf sich versteht man eine Zuordnung, die einem Punkt von E mindestens einen Punkt von E zuordnet, wobei auch sein darf. Man nennt P Originalpunkt und Bildpunkt bezüglich T. Man schreibt und liest „ ist Bildpunkt von P bei der Abbildung T“ oder „T ordnet dem Punkt P den Punkt zu“. Die Variable T steht für eine Vorschrift, nach der man den zu einem Originalpunkt P gehörenden Bildpunkt finden oder konstruieren kann.
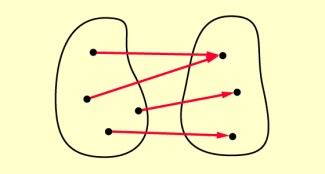
- Ist jedem P genau ein zugeordnet, so ist die Abbildung eindeutig. Veranschaulicht man die Zuordnung durch Pfeile vom Original- zum Bildpunkt, so geht von jedem Originalpunkt genau ein Pfeil aus. Allerdings können mehrere Pfeile im gleichen Bildpunkt enden.
-
Eindeutige Abbildung
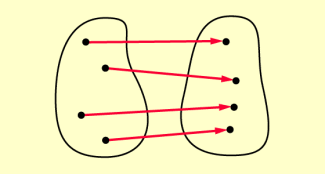
- Gilt außerdem, dass es zu jedem Bildpunkt genau einen Originalpunkt gibt, dass also nicht zwei Pfeilspitzen im selben Punkt enden, so ist die Abbildung umkehrbar eindeutig – man kann gewissermaßen die Rolle von Original- und Bildpunkt vertauschen und diese neue Abbildung ist ebenfalls eindeutig. Solche Abbildungen heißen auch eineindeutig.
-
Eineindeutige Abbildung
Konstruktive Definition (der Abbildung) und Grundaufgaben
Im Folgenden wird eine umkehrbar eindeutige Abbildung der Ebene auf sich betrachtet und eine konstruktive Definition dafür angegeben.
In E seien eine Gerade g und eine Parallelgeradenschar, deren Geraden nicht parallel zu g sind, gegeben.
Die Abbildungs- oder Zuordnungsvorschrift, mit der zu einem Punkt P sein Bildpunkt konstruiert werden kann, laute:
- Ist , so ist .
(Mit anderen Worten: Jeder Punkt auf g bleibt bei der Abbildung fest, ist ein Fixpunkt; g ist eine Fixpunktgerade.)
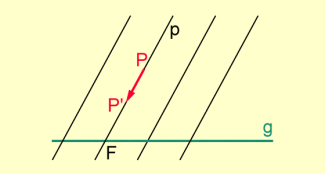
- Liegt P auf einer Geraden p der Parallelgeradenschar, so soll auch auf p liegen, und ist , so gelte mit .
(Mit anderen Worten: Original- und Bildpunkte bilden jeweils mit den Schnittpunkten ihrer Trägergeraden mit der Fixpunktgeraden ein konstantes Teilverhältnis.)
-
Konstruktive Definition der Abbildung
Diese Erklärung ermöglicht, mithilfe der Strahlensätze zu jedem P aus E das zugehörige zu konstruieren, wenn außer g entweder k und die Parallelgeradenschar oder ein Punktepaar gegeben sind.
Im Folgenden soll die Zuordnung von P zu immer durch einen Pfeil veranschaulicht werden, der von P nach zieht (verläuft). Alle Pfeile der konstruktiv definierten Abbildung liegen auf den Geraden der Parallelgeradenschar. Die Richtung der Geraden der Parallelgeradenschar heißt die Streichrichtung der Abbildung.
Grundaufgabe 1
Es seien g und mit sowie Q gegeben.
Gesucht ist .
1. Fall:
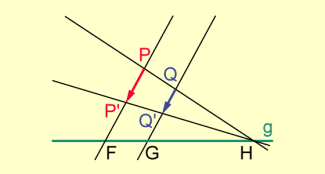
Man zeichnet die Gerade PQ. Es sei . Man zeichnet . Die Parallele zu durch Q schneidet in und g in G.
Nach Strahlensatz gilt .
-
Konstruktion von Abbildungen: Grundaufgabe 1; 1.Fall
2. Fall:
Man konstruiert für einen beliebigen Punkt M, der nicht auf liegt, den Punkt und sodann mit den Bildpunkt (wie im 1. Fall beschrieben). Der Strahlensatz garantiert die Teilverhältnisgleichheit.
-
Konstruktion von Abbildungen: Grundaufgabe 1; 2.Fall
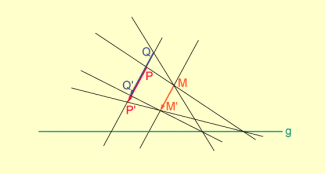
3. Fall:
liegt auf der Streichrichtungsgeraden durch Q und der Parallelen zu PQ durch . Die Parallelität von PQ, und g einerseits sowie und andererseits garantiert die Teilverhältnisgleichheit.
-
Konstruktion von Abbildungen: Grundaufgabe 1; 3.Fall
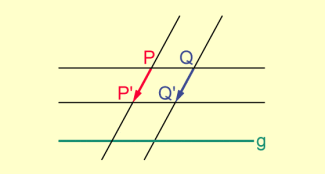
Grundaufgabe 2
Gegeben seien g, eine Streichrichtung durch p, k mit und .
Gesucht ist .
-
Konstruktion von Abbildungen: Grundaufgabe 2
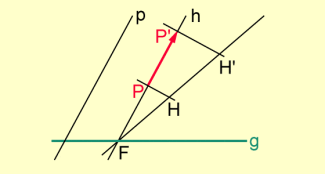
Man zeichnet die durch P gehende Streichrichtungsgerade h. Es sei .
Man zeichnet eine beliebige Gerade durch F und auf ihr H und so, dass ist. Die Parallele zu PH durch schneidet h in , und es ist .
Eigenschaften der Abbildung
Aus der konstruktiven Definition liest man wesentliche Eigenschaften der Abbildung unmittelbar ab:
- Die Abbildung hat eine punktweise fest bleibende Gerade, die man auch Achse nennt.
- Verbindet man jeden Originalpunkt, der nicht auf der Achse liegt, und seinen Bildpunkt durch einen Pfeil, so liegen alle diese Pfeile auf den Streichrichtungsgeraden der Abbildung, sind also zueinander parallel.
- Die Anfangs- und Endpunkte eines jeden Pfeils bilden mit dem Schnittpunkt seiner Trägergeraden mit der Abbildungsachse ein- und dasselbe Teilverhältnis.
- Jeder Punkt hat genau ein Bild und jeder Bildpunkt hat genau ein Original. Von jedem Punkt geht genau ein Pfeil aus und es gibt keinen Punkt, in dem zwei Pfeile enden. Die Abbildung ist umkehrbar eindeutig.
- Für k = 1 ist , d.h. . Diese Abbildung lässt alle Punkte fest, es ist die sogenannte identische Abbildung oder Identität.
- Für liegen Original- und Bildpunkte auf derselben Seite der Abbildungsachse, für auf verschiedenen Seiten.
Aus der konstruktiven Definition kann man aber auch noch weitere wichtige Eigenschaften ableiten.
- Das Bild einer Geraden ist wieder eine Gerade.
Für die Achse der Abbildung und ihre Streichrichtungsgeraden ist dies anschaulich klar. Auch die Streichrichtungsgeraden werden auf sich selbst abgebildet, gehen in sich selbst über, wenn sie auch nicht punktweise fest bleiben. Es sind sogenannte Fixgeraden oder Ruhegeraden.
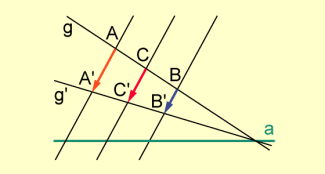
Die Punkte A und B, die auf einer Geraden g liegen, die nicht Streichrichtungsgerade und nicht Achse der Abbildung ist, werden auf die Punkte A' und B' abgebildet, die ihrerseits eine Gerade bestimmen. Wählt man auf g einen beliebigen Punkt C und bildet diesen ab, so muss sein Bild wegen der Teilverhältnistreue der Abbildung auf liegen.
-
Eigenschaften der Abbildung (1)
- Wenn zwei Originalgeraden parallel sind, so sind es auch ihre Bilder:
Für die Achse der Abbildung und ihre Streichrichtungsgeraden ist dies wieder anschaulich klar.
Sind die Geraden g und h untereinander und zur Achse a von T parallel, so sind wegen der Teilverhältniskonstanz von T sowohl als auch zu a und damit untereinander parallel.
-
Eigenschaften der Abbildung (2)
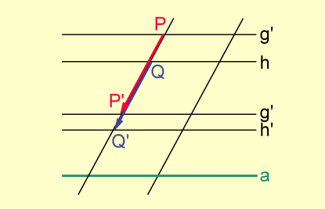
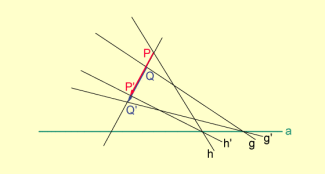
Auch im Fall, dass , aber ist, gilt ; denn hätten und einen gemeinsamen Punkt , so wäre sowohl das Bild eines Punktes von g als auch das Bild eines Punktes von h, d.h., in Q' würden zwei Pfeile der Abbildung enden. Das ist aber wegen der Eineindeutigkeit der Abbildung ausgeschlossen.
-
Eigenschaften der Abbildung (3)
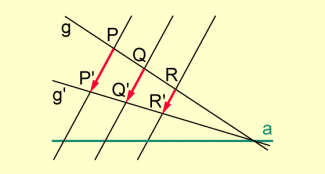
- Das Teilverhältnis dreier Punke auf einer Geraden bleibt bei der Abbildung erhalten:
(Mit anderen Worten: Das Teilverhältnis dreier Punkte auf einer beliebigen Geraden ist eine Invariante der Abbildung.)
Liegen die Punkte P, Q und R auf g, so liegen ihre Bildpunkte auf und wegen der Parallelität der Pfeile und ist gesichert, dass ist.
-
Eigenschaften der Abbildung (4)
Definition der affinen Abbildung
Eine punktweise Abbildung der Ebene auf sich, die
1. Geraden in Geraden überführt,
2. parallele Geraden in parallele Geraden überführt und
3. teilverhältnistreu ist,
heißt affine Abbildung oder Affinität.
Die oben beschriebene, konstruktiv definierte Abbildung ist eine Affinität. Sie heißt Hauptaffinität oder Achsenaffinität.
Eine affine Abbildung der Ebene ist durch die Zuordnung von drei Bildpunkten zu drei nicht auf einer Geraden liegenden Originalpunkten eindeutig bestimmt, die Hauptaffinität z.B. durch zwei Punktepaare und auf ihrer Achse, für die also und ist, sowie ein Punktepaar und . Liegen die drei Bildpunkte auf einer Geraden, so wird durch die Zuordnung eine singuläre Affinität bestimmt. Hier werden nur reguläre Affinitäten betrachtet, also solche, die durch drei Punktepaare aufgespannt sind, deren Originalpunkte wie auch die Bildpunkte sich in allgemeiner Lage befinden, also nicht alle drei jeweils auf einer Geraden liegen.
Die Kongruenz- und Ähnlichkeitsabbildungen bzw. -transformationen sind Beispiele für Affinitäten, denn die in der Definition der Affinität angeführten Eigenschaften sind sicher bei den Schiebungen, Drehungen, Spiegelungen, Schubspiegelungen, Drehstreckungen und Drehstreckspiegelungen gegeben.
Neben den Kongruenz- und Ähnlichkeitstransformationen und den Hauptaffinitäten gibt es aber noch andere affine Abbildungen der Ebene auf sich.
Ein Sonderfall der Hauptaffinität ist die Affinspiegelung. Alle ihre Pfeile werden von der Achse halbiert. Es ist wie die Orthogonalspiegelung eine involutorische Abbildung mit .
-
Affinspiegelung
Eine weitere axiale Affinität ist die Hauptscherung. Ihre Streichrichtungsgeraden sind parallel zur Achse. Sie sind flächeninhaltstreu.
-
Hauptscherung
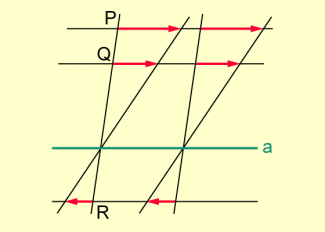
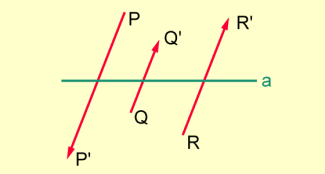
Es gibt Affinitäten, die genau einen Fixpunkt haben. Ist eine Affinität durch drei Punktepaare und in allgemeiner Lage, also drei Pfeile, aufgespannt, von denen zwei Pfeile parallel sind, so ist der Schnittpunkt der Geraden durch die Pfeilanfänge und Pfeilspitzen der parallelen Pfeile ein Fixpunkt.
-
Affinität mit genau einem Fixpunkt
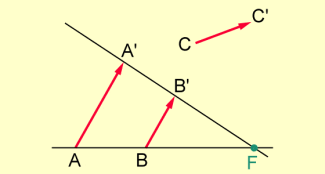
Einen weiteren Fixpunkt kann es nicht geben, denn dann hätte die Affinität eine Fixpunktgerade, wäre also eine Hauptaffinität, was deswegen ausgeschlossen ist, weil der dritte Pfeil als nicht parallel zu den beiden anderen aufspannenden Pfeilen vorausgesetzt ist.
Sind die beiden parallelen Pfeile der Aufspannung auch noch gleich lang, so schneiden sich die Geraden durch die Pfeilanfänge und -spitzen nicht, die Affinität hat keinen Fixpunkt.
-
Affinität mit keinem Fixpunkt
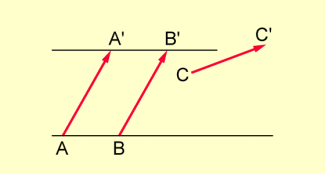
Ist die Affinität durch drei Pfeile aufgespannt, von denen keine zwei parallel sind, so sucht man zwei zu einander parallele Pfeile auf. Das gelingt immer. Hat man solche gefunden, so muss man wieder unterscheiden, ob sich die Verbindungsgeraden der Pfeilanfänge und Pfeilspitzen schneiden oder nicht. Entsprechend hat man es mit einer Affinität zu tun, die entweder genau einen Fixpunkt oder keinen Fixpunkt hat.
Affinitäten haben also
- Fixpunkte, die auf einer Fixpunktgeraden liegen;
- genau einen Fixpunkt;
- keinen Fixpunkt oder
- Fixpunkte, die die ganze Ebene erfüllen (das ist die identische Abbildung, die alle Punkte in Ruhe lässt).

