Zylinderkoordinaten

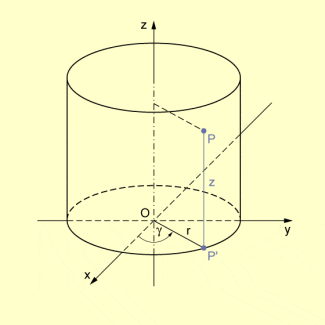
Die drei Zylinderkoordinaten eines Punktes P sind die folgenden:

1. der Radius r (mit $r\ge 0$) als Abstand des Punktes $P\text{'}$ vom Ursprung O, wobei $P\text{'}$ die Projektion von P auf die xy-Ebene (Äquatorebene) ist;
2. der vorzeichenbehaftete Abstand z des Punktes P von der xy-Ebene (Äquatorebene);
3. der Winkel $\varphi$, der zwischen der x-Achse und der Strecke $\overline{OP\text{'}}$ in der xy-Ebene gebildet wird (wobei $\varphi$ im Intervall $0\le \varphi <2\pi$ liegt)

Die folgende Tabelle gibt die Umrechnungsmöglichkeiten von kartesischen Koordinaten in Zylinderkoordinaten (und umgekehrt) an:

• Beispiel 1: Gegeben sei der Punkt $P\left(3;4;5\right)$.
  Es sind die Zylinderkoordinaten von P zu ermitteln.

Aus $x=\mathrm{3,}y=4undz=5$ ergibt sich nach Anwenden obiger Formeln:
$\begin{array}{l}r=\sqrt{9+16}=5\\ \varphi =arc\cos \frac{3}{5}=arc\sin \frac{4}{5}\approx \mathrm{53,13}°\\ z=z\end{array}$

• Beispiel 2: Gegeben sei der Punkt P mit $r=\mathrm{2,}\varphi =55°undz=4$.
  Es sind die kartesischen Koordinaten von P zu ermitteln.

Unter Anwendung obiger Formeln erhält man:
$\begin{array}{l}x=2\cdot \cos 55°\approx \mathrm{1,147}\\ y=2\cdot \sin 55°\approx \mathrm{1,638}\\ z=4\end{array}$