Beispiele mathematischer Geografie

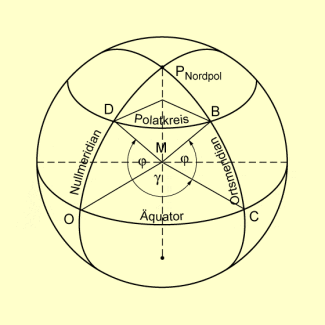
Die geografische Länge von D wird durch den Winkel $\lambda$ gemessen, den der Meridian durch D mit dem Meridian durch Greenwich, dem sogenannten Nullmeridian bildet. Sie wird von $0^{\circ }bis{180}^{\circ }$ nach Osten mit dem Vorzeichen „+“ und nach Westen und mit dem Vorzeichen „-“ bezeichnet.

Die geografische Breite von D wird durch den Winkel $\varphi$ gemessen, den der durch D gelegte Radius mit der Äquatorebene bildet. Sie wird von $0^{\circ }bis{90}^{\circ }$ mit dem Vorzeichen „+“ nach Norden und mit dem Vorzeichen „-“ nach Süden bezeichnet.

Die Länge u eines Großkreises entspricht dem Umfang der Erdkugel. Es ist $u=2r\pi ,alsou\sim 40024km$, wenn r für den Radius der Kugel steht.
Bei einem mittleren Erdradius von $6370km$ begrenzt ein Mittelpunktswinkel von $1^{\circ }$ auf einem Großkreis ein Bogenstück von $\mathrm{111,1}km$, ein Bogenstück von $1\prime$ ein Stück von $\mathrm{1,852}km$. Das ist eine sogenannte Seemeile. 4 Seemeilen sind 1 geografische Meile.

Mithilfe des Seitenkosinussatzes kann die kürzeste Entfernung zweier Orte auf der Erde berechnet werden. Die kürzeste Entfernung zweier Orte ist bestimmt durch den kürzeren Abschnitt des durch die Orte bestimmten Großkreises.

Beispiele

• Beispiel 1: Berlin hat die Koordinaten $\lambda ={\mathrm{13,4}}^{\circ },\varphi ={\mathrm{52,5}}^{\circ }$, Tokio hat die Koordinaten $\lambda ={\mathrm{139,8}}^{\circ },\varphi ={\mathrm{35,7}}^{\circ }$.
  Wie groß ist die kürzeste Entfernung Berlin - Tokio?

Berlin (B) bildet mit dem Pol (P) und Tokio (T) ein sphärisches Dreieck.

Im sphärischen Dreieck BPT gilt:
$\begin{array}{l}PB={90}^{\circ }-{\mathrm{52,5}}^{\circ }={\mathrm{37,5}}^{\circ },PT={90}^{\circ }-{\mathrm{35,7}}^{\circ }={\mathrm{54,3}}^{\circ },\\ \sphericalangle BPT={\mathrm{139,8}}^{\circ }-{\mathrm{13,4}}^{\circ }={\mathrm{126,4}}^{\circ }.\\ \cos BT=\cos PB\cdot \cos PT+\sin PB\cdot \sin PT\cdot \cos \sphericalangle BPT\\ \cos BT=\cos {\mathrm{37,5}}^{\circ }\cdot \cos {\mathrm{54,3}}^{\circ }+\sin {\mathrm{37,5}}^{\circ }\cdot \sin {\mathrm{54,3}}^{\circ }\cdot \cos {\mathrm{126,4}}^{\circ }\\ =-\mathrm{0,1358148}\Rightarrow BT={\mathrm{97,81}}^{\circ }\end{array}$

Die kürzeste Entfernung Berlin - Tokio beträgt $\mathrm{97,81}\cdot \mathrm{111,1}km$, das sind $\mathrm{10866,691}\text{km.}$

• Beispiel 2: Das australische Sydney hat die Koordinaten $\lambda ={\mathrm{151,7}}^{\circ }$ und $\varphi ={\mathrm{33,9}}^{\circ }$. Wie groß ist die kürzeste Entfernung Berlin (B) - Sydney (S)?

Es gilt:
$BT={90}^{\circ }-{\mathrm{52,5}}^{\circ }={\mathrm{37,5}}^{\circ },SP={90}^{\circ }+{\mathrm{33,9}}^{\circ }={\mathrm{123,9}}^{\circ }$ und $\sphericalangle BPS={\mathrm{151,7}}^{\circ }-{\mathrm{13,4}}^{\circ }={\mathrm{138,3}}^{\circ }$.
$\begin{array}{l}\cos BS=\cos {\mathrm{37,5}}^{\circ }\cdot \cos {\mathrm{123,9}}^{\circ }+\sin {\mathrm{37,5}}^{\circ }\cdot \sin {\mathrm{123,9}}^{\circ }\cdot \cos {\mathrm{138,3}}^{\circ }\\ =-\mathrm{0,8197498}\Rightarrow BS={\mathrm{145,06}}^{\circ }\end{array}$

Die kürzeste Entfernung Berlin - Sydney beträgt $\mathrm{145,06}\cdot \mathrm{111,1}km$, das sind $\mathrm{16116,166}km$.

• Beispiel 3: Buenos Aires hat die Koordinaten $\lambda =-{\mathrm{34,6}}^{\circ },\varphi =-{\mathrm{58,37}}^{\circ }$. Wie groß ist die kürzeste Entfernung Berlin (B) - Buenos Aires (A)?

Es gilt:
$\begin{array}{l}BP={90}^{\circ }-{\mathrm{52,5}}^{\circ }={\mathrm{37,5}}^{\circ },\\ AP={90}^{\circ }+{\mathrm{34,6}}^{\circ }={\mathrm{124,6}}^{\circ },\\ \sphericalangle APB={\mathrm{58,37}}^{\circ }+{\mathrm{13,4}}^{\circ }={\mathrm{71,77}}^{\circ }\end{array}$
$\begin{array}{l}\cos AB=\cos {\mathrm{37,5}}^{\circ }\cdot \cos {\mathrm{124,6}}^{\circ }+\sin {\mathrm{37,5}}^{\circ }\cdot \sin {\mathrm{124,6}}^{\circ }\cdot \cos {\mathrm{71,77}}^{\circ }\\ =-{\mathrm{0,2937424}}^{\circ }\Rightarrow AB={\mathrm{107,08}}^{\circ }\end{array}$

Die kürzeste Entfernung Berlin - Buenos Aires beträgt $\mathrm{107,08}\cdot \mathrm{111,1}km$, das sind $\mathrm{11896,588}km$.

Da in den vorangestellten Beispielen jeweils die Längen aller drei Seiten der betrachteten sphärischen Dreiecke und der Winkel am Pol bekannt sind, können auch die beiden anderen Winkel – etwa $\alpha und\beta$ genannt – mithilfe des Seitenkosinussatzes oder des Sinussatzes berechnet werden. Damit kann der Kurs eines Flugzeugs, das z.B. von Buenos Aires nach Berlin auf einem Großkreis fliegen würde, beschrieben werden, wobei man zwischen Abflugkurs und Ankunftskurs unterscheiden muss. Beide sind durch die Größe der beiden Winkel bestimmt.

Im Beispiel Buenos Aires - Berlin erhält man mithilfe des Seitenkosinussatzes:
$\begin{array}{l}\cos \alpha =\frac{\cos PB-\cos PA\cdot \cos AB}{\sin PA\cdot \sin AB}=\mathrm{0,7963243,}also\alpha ={\mathrm{37,22}}^{\circ }\\ \cos \beta =\frac{\cos PA-\cos PB\cdot \cos AB}{\sin PB\cdot \sin AB}=\mathrm{0,5754335,}also\beta ={\mathrm{125,13}}^{\circ }\end{array}$

Kurse werden durch die Abweichung der Flug- bzw. Fahrtrichtung von der Nord-Süd-Richtung angegeben. Demzufolge beträgt der Abflugswinkel in Buenos Aires $N{\mathrm{37,22}}^{\circ }O$, der Ankunftswinkel des Flugzeugs in Berlin wegen ${180}^{\circ }-{\mathrm{125,13}}^{\circ }={\mathrm{54,87}}^{\circ },alsoN{\mathrm{54,87}}^{\circ }O$.
Fliegt ein Flugzeug von Berlin nach Buenos Aires, hat es einen Abflugswinkel $S{\mathrm{125,13}}^{\circ }W$ und einen Ankunftswinkel von $S{\mathrm{37,22}}^{\circ }W$.

An der Unterschiedlichkeit von Abflugs- und Ankunftskurs sieht man anschaulich, dass ein Flugzeug oder Schiff, das auf einem Großkreis fliegt oder fährt, sich nicht mit konstantem Kurs bewegen kann, sondern in jedem Moment seinen Kurs ändern muss, soll es auf dem Großkreis, also der Strecke kürzester Entfernung bleiben. In der Praxis fliegen Flugzeuge oder Schiffe auf einer Linie konstanten Kurses, einer sogenannten Loxodrome, oder auf einer geeigneten Zusammensetzung günstiger Abschnitte von Loxodromen, die das Navigieren erleichtern oder erst möglich machen, wenn dadurch auch der zurückzulegende Weg länger wird als er auf dem Großkreis wäre.

Die Zeitzonen betragen 15 Längengrade. Der Zeitunterschied zwischen Tokio, Sydney, Buenos Aires und Berlin errechnet sich aus der Differenz bzw. der Summe der zu den Städten gehörenden Längengrade. Er beträgt gegenüber der mitteleuropäischen Zeit zwischen Tokio und Berlin acht Stunden, zwischen Sydney und Berlin neun Stunden und zwischen Berlin und Buenos Aires fünf Stunden.