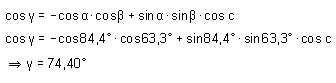Das sphärische oder das Kugeldreieck
Die sphärische Geometrie ist die Geometrie auf der Kugel, die sphärische Trigonometrie die Trigonometrie der Kugeloberfläche. Dass beide von der Geometrie und der Trigonometrie der Ebene verschieden sein müssen, erkennt man schon daran, dass es auf der Kugel keine Geraden im Sinne der klassischen ebenen Geometrie und Trigonometrie gibt.
Im Weiteren werden Kugeldreiecke definiert und insbesondere eulersche Dreiecke betrachtet. Zur Berechnung sphärischer Dreiecke werden u.a. der sphärische Sinussatz, der Winkelkosinussatz und der Seitenkosinussatz verwendet.
Drei Punkte A, B und C einer Kugel, die nicht auf ein und derselben Kugelgeraden liegen, bestimmen drei Kugelgeraden. Auf diesen liegen die sphärischen Strecken bzw. Abstände . Diese Strecken sind höchstens gleich . Sie bilden ein sphärisches oder Kugeldreieck.
![]()
Man kann ein leicht zu überschauendes Beispiel dafür angeben, dass die Summe der Innenwinkelgrößen eines Kugeldreiecks größer als ist:
![]()
Ist eine Strecke auf dem Äquator und sind , wo P für einen Erdpol steht, Strecken auf Meridianen, so ist schon die Summe der Winkel . Für jedes echte Dreieck ist die Winkelsumme also größer als . Man sieht am Beispiel auch, dass sie kleiner als sein muss.
Im Weiteren werden nur solche Kugeldreiecke betrachtet, deren Flächeninhalt kleiner als der einer Halbkugel ist und deren Seiten und Winkel alle jeweils kleiner als sind. Sie heißen eulersche Dreiecke.
Bezeichnungen:
Wie in der klassischen Geometrie heißen die Seiten des Kugeldreiecks AB, BC, CA bzw. c, a, b. Deren Längen werden mithilfe der zughörigen Zentriewinkel ausgedrückt.
So ist die Länge der Seite a gleich dem im Grad- oder Bogenmaß gemessenen Winkel , wo M für den Mittelpunkt der Kugel steht, also .
Analog ist und .
Die Winkel werden von den Tangenten an die Kugelgeraden in den Punkten A, B und C bzw. den Neigungswinkeln der zugehörigen Ebenen gebildet.
Die Kugelgeraden oder Großkreise sind von ihren Polen aus gesehen im Gegenuhrzeigersinn orientiert, die Winkel sind entsprechend durch Drehung des einen Schenkels auf den anderen bestimmt.
Zu den Ecken A, B, C gehören die Gegenecken zu Dreieck ABC das Gegendreieck
![]()
Zum Dreieck ABC gehören die Nebendreiecke , die es zu je einem Kugelzweieck ergänzen.
Die Nebendreiecke des Gegendreiecks heißen Scheiteldreiecke.
Um den Flächeninhalt eines sphärischen Dreiecks zu berechnen, werden aus dem Dreieck und geeigneten Gegen- und Nebendreiecken Zweiecke gebildet, deren Flächeninhalte bestimmt werden können.
Das Dreieck ABC bildet zusammen mit dem Nebendreieck ein Zweieck mit dem Flächeninhalt .
Ebenso bilden die Dreieck ABC und sowie ABC und Zweiecke mit dem Öffnungswinkel , sodass man schreiben kann:
,
,
.
Addiert man die linken und die rechten Seiten und ersetzt dabei das Dreieck durch das Dreieck , das mit in allen Seitenlängen und Winkelgrößen übereinstimmt, symmetrisch zu ist und den gleichen Flächeninhalt hat, so erhält man:
In der Klammer steht nun die Fläche einer Halbkugel, also .
Nach einigen Umformungen erhält man:
Die Summe heißt sphärischer Exzess. Das ist der Überschuss der Innenwinkelsumme des sphärischen Dreiecks über . Man bezeichnet diese Summe mit , so dass man für den Flächeninhalt f eines sphärischen Dreiecks kürzer schreiben kann:
Um Möglichkeiten der Berechnung von Seitenlängen und Winkelgrößen von sphärischen Dreiecken zu finden, kann man wie in der ebenen Trigonometrie vorgehen. Man betrachtet zunächst ein rechtwinkliges sphärisches Dreieck, um die Beziehungen zwischen den Seiten und Winkeln dieses Dreiecks zu bestimmen und wendet sodann die gefundenen Relationen auf ein schiefwinkliges Dreieck an.
Als Hilfsfigur verwendet man ein sogenanntes Dreikant.
Verbindet man die Ecken eines sphärischen Dreiecks ABC mit dem Mittelpunkt M der Kugel, so bilden die Verbindungsgeraden ein Dreikant. Den Seiten des Dreiecks entsprechen die Kantenwinkel des Dreikants. Sie heißen darum auch Seiten des Dreikants. Den Winkeln des Dreiecks entsprechen die Winkel zwischen den Ebenen, welche das Dreikant bilden. Sie heißen darum auch Winkel des Dreikants.
Das rechtwinklige sphärische Dreieck
Ist das sphärische Dreieck ABC ein bei C rechtwinkliges sphärisches Dreieck, erhält man aus nebenstehender Figur:
![]()
Sind also von einem rechtwinkligen sphärischen Dreieck jeweils zwei der in den vorstehenden Gleichungen enthaltenen Stücke bekannt, können die anderen Stücke berechnet werden.
- Beispiel: Bekannt sind .
Aus .
Aus , also .
Das Dreieck hat den sphärischen Exzess .
Sein Flächeninhalt beträgt .
Das schiefwinklige sphärische Dreieck
Ein schiefwinkliges sphärisches Dreieck wird berechnet, indem man durch eine Höhe zwei rechtwinklige Dreiecke erzeugt und diese Höhe mithilfe der rechtwinkligen Dreiecke durch geeignete Winkelfunktionen ausdrückt.
![]()
Das Dreieck ABC wird durch die Höhe in die rechtwinkligen Dreiecke ADC und ADB zerlegt. Dann gilt:
Analog erhält man mithilfe von .
Beide Proportionen fasst man zur fortlaufenden Proportion
zusammen.
Das Ergebnis ist der sphärische Sinussatz:
- Satz (Sphärischer Sinussatz): Im Kugeldreieck verhalten sich die Sinus zweier Seiten wie die Sinus der Gegenwinkel.
Der Fall, dass die Höhe außerhalb des Dreiecks ABC liegt, führt wegen auf das gleiche Resultat.
![]()
Sind also von einem sphärischen Dreieck zwei Seiten und der Gegenwinkel einer dieser Seiten oder zwei Winkel und die Gegenseite eines der Winkel gegeben, so kann der andere Winkel bzw. die andere Gegenseite berechnet werden.
- Beispiel 1: Gegeben sind .
Aus dem Sinussatz folgt:
und hieraus .
Wegen muss sein, also ist nur Lösung der Aufgabe.
Es gibt nur ein Dreieck mit diesen Seiten und Winkeln.
- Beispiel 2: Gegeben sind .
Mit erhält man und hieraus .
Da sein muss, sind beide Werte Lösungen der Aufgabe.
Es gibt zwei Dreiecke mit diesen Seiten und Winkeln.
- Beispiel 3: Gegeben sind .
Man erhält , d.h. es gibt kein eulersches Dreieck mit den gegebenen Maßen.
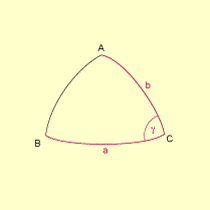
Aus der nebenstehenden Figur erhält man den Seitenkosinussatz.
![]()
Es gilt:
Wegen ist also .
Damit geht der Quotient über in .
Hieraus erhält man .
Durch zyklische Vertauschung erhält man die restlichen Formeln des Seitenkosinussatzes:
- Satz (Seitenkosinussatz): Im sphärischen Dreieck ist der Kosinus einer Seite gleich der Summe der Kosinusprodukte der beiden anderen Seiten und dem mit dem Kosinus des eingeschlossenen Winkels multiplizierten Sinusprodukt dieser Seiten.
Der Seitenkosinussatz ermöglicht also die Berechnung der Länge einer Seite, wenn die Längen der beiden anderen Seiten und der von ihnen eingeschlossene Winkel gegeben sind. Stellt man die Formeln nach dem in ihnen vorkommenden Winkelkosinus um, so erkennt man, dass sie zur Berechnung der Größe eines Winkels geeignet sind, wenn man die Längen aller Seiten kennt.
Geht man zum Polardreieck des Dreiecks ABC über, indem man a, b, c, C durch A, B, C und c ersetzt, erhält man den Winkelkosinussatz:
- Satz (Winkelkosinussatz): Im sphärischen Dreieck ist der Kosinus eines Winkels gleich der Summe aus dem negativen Produkt der Kosinus der beiden anderen Winkel und dem mit dem Kosinus der gegenüberliegenden Seite multiplizierten Sinusprodukt der beiden anderen Winkel.
Der Winkelkosinussatz ermöglicht also die Berechnung der Größe eines Winkels, wenn die beiden anderen Winkel und die Länge der dem Winkel gegenüberliegenden Seite bekannt sind. Er ermöglicht auch die Berechnung der Länge einer Seite, wenn alle Winkel des sphärischen Dreiecks gegeben sind.
- Beispiel 4: Gegeben sind: .
Stellt man den Seitenkosinussatz nach um, erhält man:
Aus
und aus .
Anmerkung: Man kann zur Berechnung von und auch den Sinussatz heranziehen. Man erhält jeweils zwei mögliche Winkelwerte, die man daraufhin überprüfen muss, ob sie für eulersche Dreiecke möglich sind. So erhält man z.B. mithilfe des Sinussatzes für auch . Aber die Summe der Winkelgrößen des Dreiecks ist für diesen Wert von kleiner als . Ein solches Dreieck gibt es nicht. Der Seitenkosinussatz ist zwar rechnerisch aufwendiger, da die Kosinuswerte für Winkel kleiner positiv, für Winkel größer als und kleiner als aber negativ sind, liefert er jedoch immer eindeutige Lösungen.
- Beispiel 5: Gegeben sind .
Aus dem Seitenkosinussatz wird c berechnet:
Nun sind a, b und c bekannt, also können und mithilfe der entsprechenden Formeln des Kosinussatzes berechnet werden.
Berechnet man mithilfe des Sinussatzes, erhält man die Winkelwerte .
Wegen muss auch sein, also kommt der Wert nicht infrage.
Analoges gilt für die Berechnung des Winkels .
Zur Lösung der folgenden beiden Aufgaben werden nur die Winkelkosinussätze verwendet.
- Beispiel 6: Gegeben sind , gesucht sind a, b, c.
Lösung:
- Beispiel 7: Gegeben sind ,
gesucht sind a, b, .
Lösung: