Polarkoordinatensystem
Ein Punkt der Ebene kann durch die Angabe von zwei Koordinaten im kartesischen Koordinatensystem, einem geordneten Zahlenpaar , eindeutig beschrieben werden.
Eine weitere Möglichkeit stellt die folgende Vorgehensweise dar:
Ein Ursprungspunkt O wird beliebig festgelegt. Von diesem ausgehend wird ein Strahl gezeichnet. Nun beschreiben der Abstand r des Punktes P von O und der Drehwinkel mit , um den der Strahl aus seiner Ursprungslage bis zum Punkt P werden muss, die Lage des Punktes P eineindeutig.
![]()
Im Polarkoordinatensystem wird also die Lage eines Punktes beschrieben durch:
- die Maßzahl einer Strecke, den Abstand r der Punkte O und P;
- die Maßzahl eines Winkels, den Drehwinkel des Koordinatenstrahls
-
Kartesische Koordinaten und Polarkoordinaten eins Punktes O
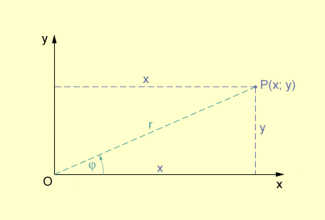
- Unter den Polarkoordinaten eines Punktes P versteht man ein Zahlenpaar , wobei r den Abstand des Punktes P vom Koordinatenursprung O sowie den Winkel zwischen x-Achse und dem Strahl OP angibt.
Die folgende Tabelle gibt die Umrechnungsmöglichkeiten von kartesischen Koordinaten in Polarkoordinaten (und umgekehrt) an:
| Kartesische Koordinaten | Polarkoordinaten |
- Beispiel 1: Es sind die Polarkoordinaten des Punktes anzugeben.
Aus ergibt sich durch Anwenden obiger Formeln:
- Beispiel 2: Gegeben seien mit die Polarkoordinaten eines Punktes P. Es sind die kartesischen Koordinaten von P zu ermitteln.
Mithilfe obiger Umrechnungsformeln erhält man:

