Definition der Kegelschnitte
Als Kegelschnitte bezeichnet man Kurven, die beim Schnitt eines geraden Doppelkreiskegels (Rotationskegels) mit einer Ebene entstehen.
-
Schnitt eines Rotationskegels mit einer Ebene (Ellipse als Schnittfigur)
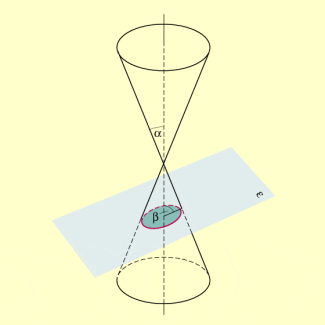
In Abhängigkeit vom Neigungswinkel der Schnittebene in Bezug auf den halben Öffnungswinkel des Kegels ergeben sich die folgenden (regulären) Kegelschnitte:
- Ellipse
Spezialfall: Kreis - Parabel
- Hyperbel
Anmerkung: Verläuft die Schnittebene durch die Spitze S des Doppelkegels, entstehen entartete Kegelschnitte (Geradenpaar bzw. Punkt).
![]()
Die folgende Abbildung zeigt nochmals das Entstehen der Kegelschnitte Kreis, Ellipse, Parabel und Hyperbel (wobei hier nicht auf den halben Öffnungswinkel , sondern auf den Neigungswinkel der Mantellinie gegenüber der Grundfläche Bezug genommen wird).
![]()
Definition der Kegelschnitte als geometrischer Ort und ihre Fadenkonstruktionen
- Der Kreis ist der geometrische Ort aller Punkte der Ebene, die von einem festen Punkt, dem Mittelpunkt M, den gleichen Abstand (Radius r) besitzen.
Fadenkonstruktion: Ein Faden der Länge r wird am Mittelpunkt M festgehalten. Ein Schreibstift am gespannten Faden beschreibt dann einen Kreisbogen.
![]()
- Die Ellipse ist der geometrische Ort aller Punkte der Ebene, für die die Summe der Abstände von zwei festen Punkten, den Brennpunkten , konstant ist.
Fadenkonstruktion: Ein Faden der Länge (2e Abstand der Brennpunkte) wird in befestigt. Ein Schreibstift am gespannten Faden beschreibt dann die Ellipse (Gärtnerkonstruktion).
![]()
- Die Parabel ist der geometrische Ort aller Punkte der Ebene, deren Abstände von einem festen Punkt (dem Brennpunkt F) und einer Geraden (der Leitlinie l) konstant sind.
Fadenkonstruktion: Ein Faden wird im Brennpunkt F und am Ende eines Schenkels eines rechtwinkligen Dreiecks befestigt. Der andere Schenkel liegt auf der Leitlinie. Der Schreibstift wird mit gespannten Faden entlang des Schenkels geführt und beschreibt die Parabel.
![]()
- Die Hyperbel ist der geometrische Ort aller Punkte der Ebene, für die die Differenz der Abstände von zwei festen Punkten, den Brennpunkten konstant ist.
Fadenkonstruktion: Ein Stab der Länge l wird am Brennpunkt drehbar befestigt. Ein Faden der Länge wird am anderen Ende des Stabes und in befestigt. Der Schreibstift wird mit dem gespannten Faden am Stab entlang geführt und beschreibt dabei einen Hyperbelast.
![]()

